Clustering multilayer graphs with missing nodes
Paper and Code
Mar 04, 2021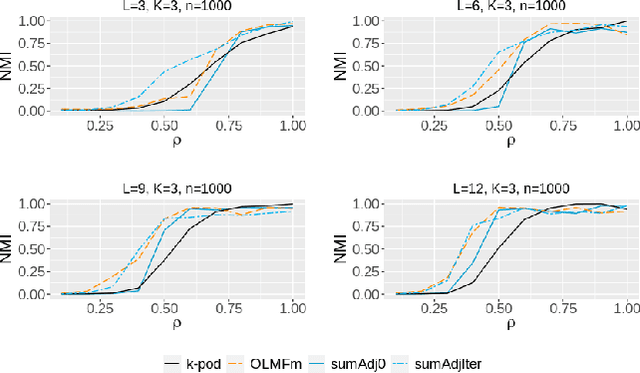
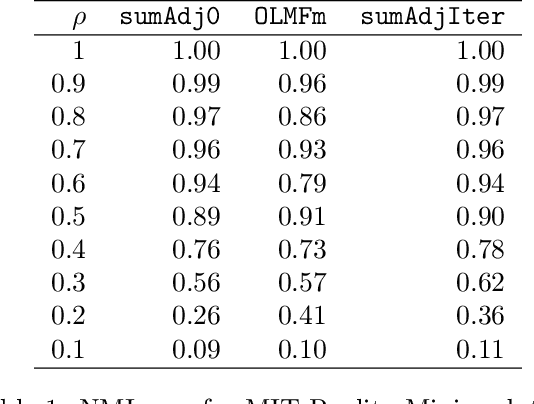
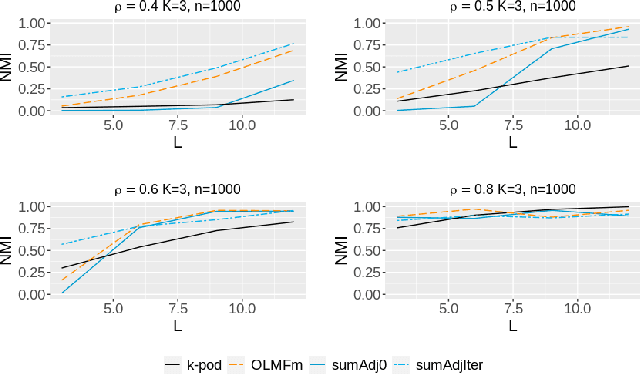
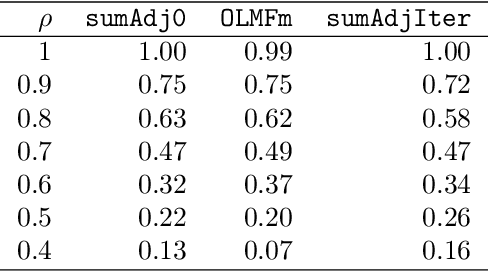
Relationship between agents can be conveniently represented by graphs. When these relationships have different modalities, they are better modelled by multilayer graphs where each layer is associated with one modality. Such graphs arise naturally in many contexts including biological and social networks. Clustering is a fundamental problem in network analysis where the goal is to regroup nodes with similar connectivity profiles. In the past decade, various clustering methods have been extended from the unilayer setting to multilayer graphs in order to incorporate the information provided by each layer. While most existing works assume - rather restrictively - that all layers share the same set of nodes, we propose a new framework that allows for layers to be defined on different sets of nodes. In particular, the nodes not recorded in a layer are treated as missing. Within this paradigm, we investigate several generalizations of well-known clustering methods in the complete setting to the incomplete one and prove some consistency results under the Multi-Layer Stochastic Block Model assumption. Our theoretical results are complemented by thorough numerical comparisons between our proposed algorithms on synthetic data, and also on real datasets, thus highlighting the promising behaviour of our methods in various settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge