Unsupervised Text Segmentation via Kernel Change-Point Detection on Sentence Embeddings

Unsupervised text segmentation is crucial because boundary labels are expensive, subjective, and often fail to transfer across domains and granularity choices. We propose Embed-KCPD, a training-free method that represents sentences as embedding vectors and estimates boundaries by minimizing a penalized KCPD objective. Beyond the algorithmic instantiation, we develop, to our knowledge, the first dependence-aware theory for KCPD under $m$-dependent sequences, a finite-memory abstraction of short-range dependence common in language. We prove an oracle inequality for the population penalized risk and a localization guarantee showing that each true change point is recovered within a window that is small relative to segment length. To connect theory to practice, we introduce an LLM-based simulation framework that generates synthetic documents with controlled finite-memory dependence and known boundaries, validating the predicted scaling behavior. Across standard segmentation benchmarks, Embed-KCPD often outperforms strong unsupervised baselines. A case study on Taylor Swift's tweets illustrates that Embed-KCPD combines strong theoretical guarantees, simulated reliability, and practical effectiveness for text segmentation.

Dynamics of "Spontaneous" Topic Changes in Next Token Prediction with Self-Attention

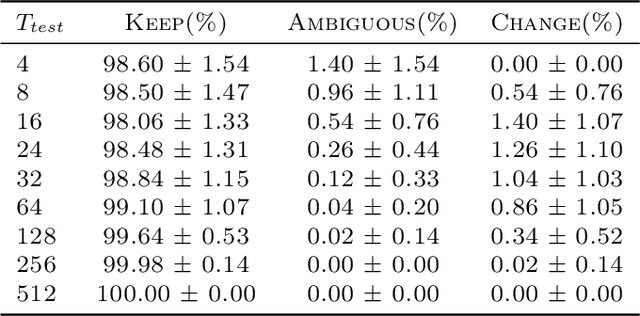
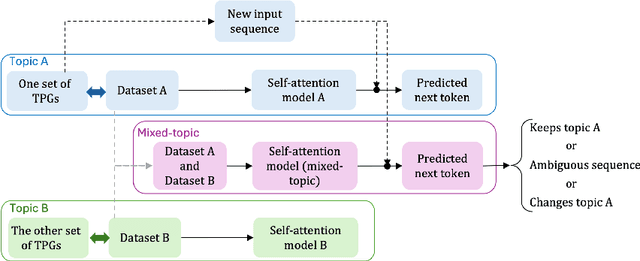
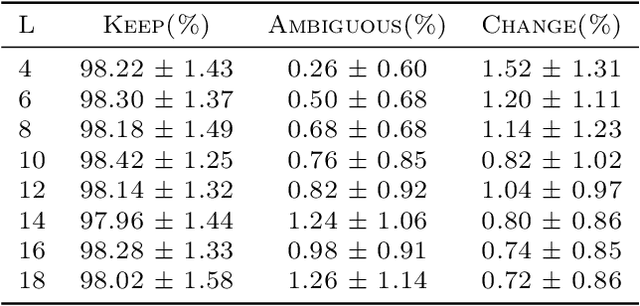
Human cognition can spontaneously shift conversation topics, often triggered by emotional or contextual signals. In contrast, self-attention-based language models depend on structured statistical cues from input tokens for next-token prediction, lacking this spontaneity. Motivated by this distinction, we investigate the factors that influence the next-token prediction to change the topic of the input sequence. We define concepts of topic continuity, ambiguous sequences, and change of topic, based on defining a topic as a set of token priority graphs (TPGs). Using a simplified single-layer self-attention architecture, we derive analytical characterizations of topic changes. Specifically, we demonstrate that (1) the model maintains the priority order of tokens related to the input topic, (2) a topic change occurs only if lower-priority tokens outnumber all higher-priority tokens of the input topic, and (3) unlike human cognition, longer context lengths and overlapping topics reduce the likelihood of spontaneous redirection. These insights highlight differences between human cognition and self-attention-based models in navigating topic changes and underscore the challenges in designing conversational AI capable of handling "spontaneous" conversations more naturally. To our knowledge, this is the first work to address these questions in such close relation to human conversation and thought.

Quantile universal threshold: model selection at the detection edge for high-dimensional linear regression

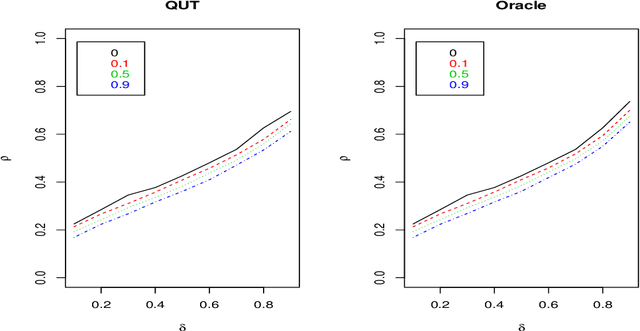
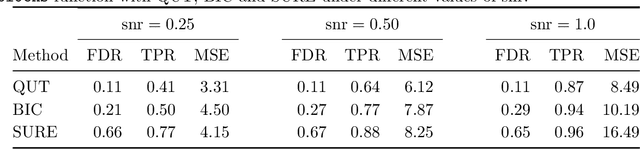
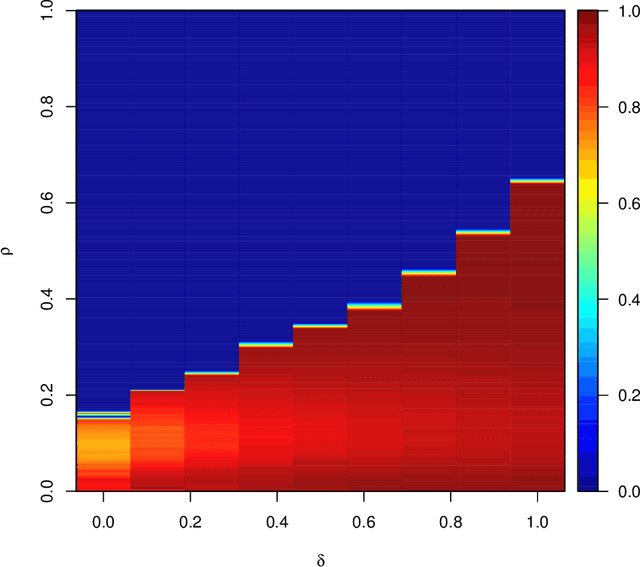
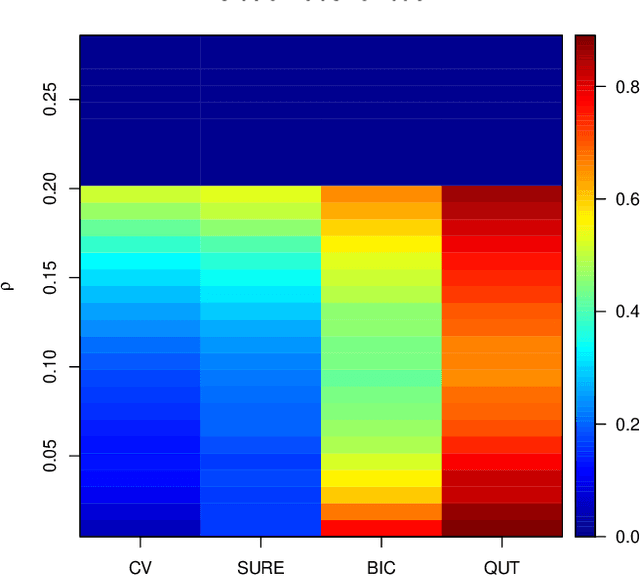
To estimate a sparse linear model from data with Gaussian noise, consilience from lasso and compressed sensing literatures is that thresholding estimators like lasso and the Dantzig selector have the ability in some situations to identify with high probability part of the significant covariates asymptotically, and are numerically tractable thanks to convexity. Yet, the selection of a threshold parameter $\lambda$ remains crucial in practice. To that aim we propose Quantile Universal Thresholding, a selection of $\lambda$ at the detection edge. We show with extensive simulations and real data that an excellent compromise between high true positive rate and low false discovery rate is achieved, leading also to good predictive risk.