Training a neural netwok for data reduction and better generalization
Paper and Code
Nov 26, 2024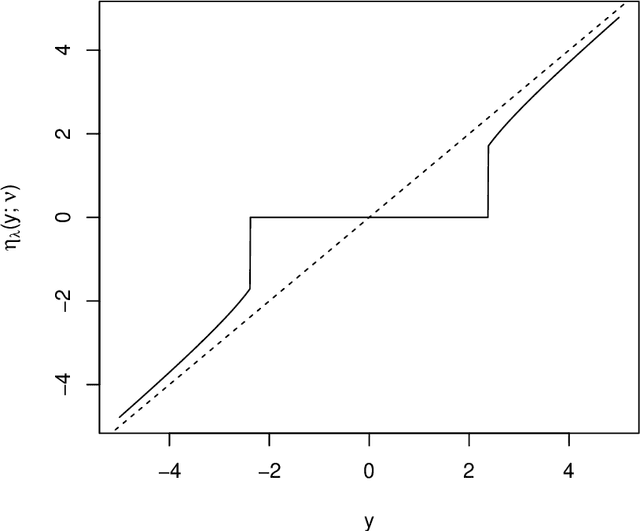

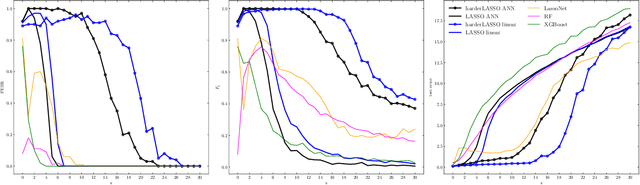
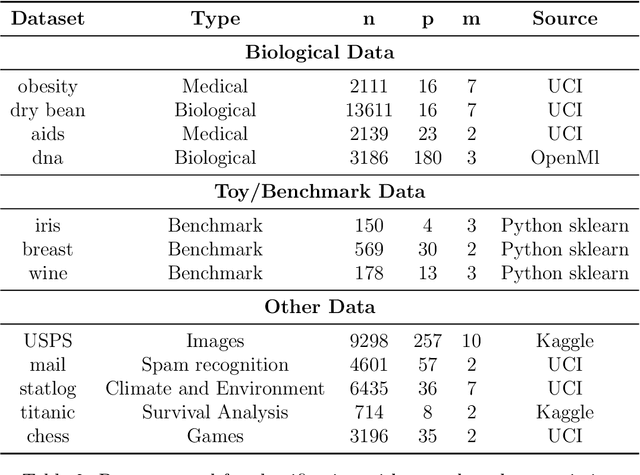
The motivation for sparse learners is to compress the inputs (features) by selecting only the ones needed for good generalization. Linear models with LASSO-type regularization achieve this by setting the weights of irrelevant features to zero, effectively identifying and ignoring them. In artificial neural networks, this selective focus can be achieved by pruning the input layer. Given a cost function enhanced with a sparsity-promoting penalty, our proposal selects a regularization term $\lambda$ (without the use of cross-validation or a validation set) that creates a local minimum in the cost function at the origin where no features are selected. This local minimum acts as a baseline, meaning that if there is no strong enough signal to justify a feature inclusion, the local minimum remains at zero with a high prescribed probability. The method is flexible, applying to complex models ranging from shallow to deep artificial neural networks and supporting various cost functions and sparsity-promoting penalties. We empirically show a remarkable phase transition in the probability of retrieving the relevant features, as well as good generalization thanks to the choice of $\lambda$, the non-convex penalty and the optimization scheme developed. This approach can be seen as a form of compressed sensing for complex models, allowing us to distill high-dimensional data into a compact, interpretable subset of meaningful features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge