Attractor learning for spatiotemporally chaotic dynamical systems using echo state networks with transfer learning

In this paper, we explore the predictive capabilities of echo state networks (ESNs) for the generalized Kuramoto-Sivashinsky (gKS) equation, an archetypal nonlinear PDE that exhibits spatiotemporal chaos. We introduce a novel methodology that integrates ESNs with transfer learning, aiming to enhance predictive performance across various parameter regimes of the gKS model. Our research focuses on predicting changes in long-term statistical patterns of the gKS model that result from varying the dispersion relation or the length of the spatial domain. We use transfer learning to adapt ESNs to different parameter settings and successfully capture changes in the underlying chaotic attractor.

Using Echo-State Networks to Reproduce Rare Events in Chaotic Systems

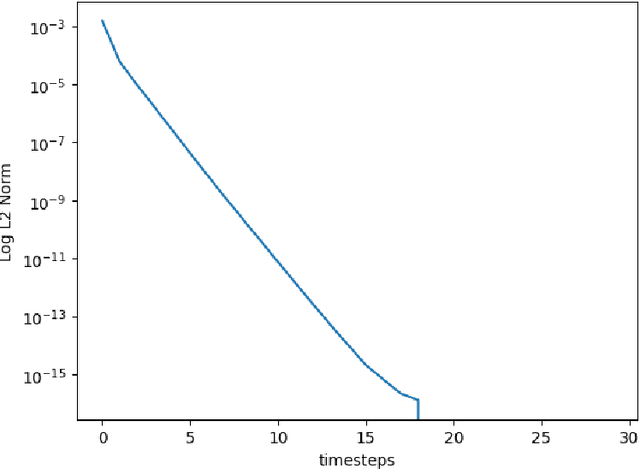
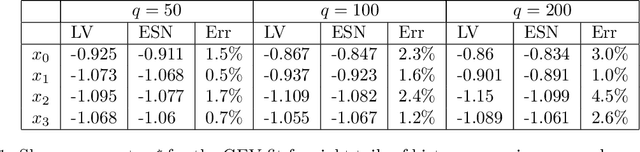
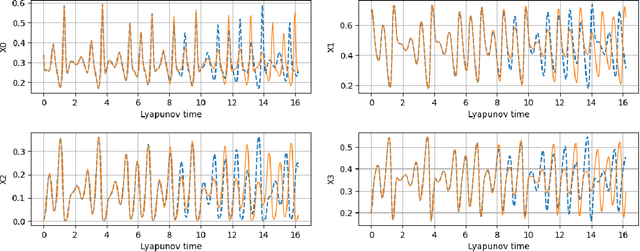
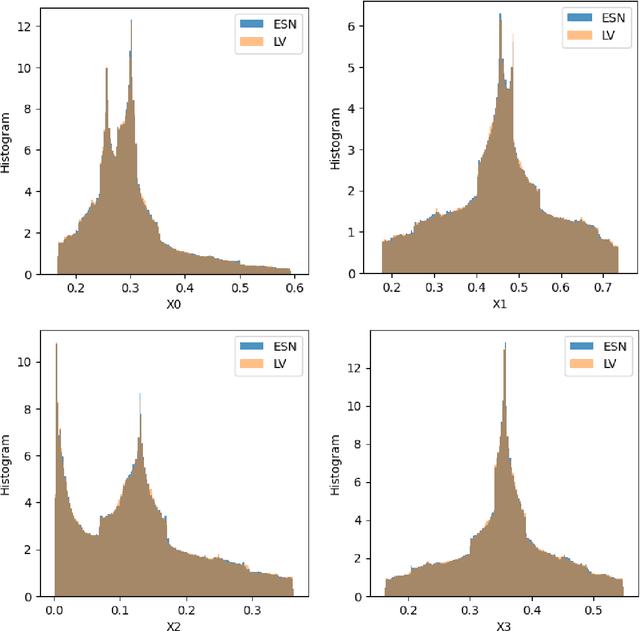
We apply the Echo-State Networks to predict the time series and statistical properties of the competitive Lotka-Volterra model in the chaotic regime. In particular, we demonstrate that Echo-State Networks successfully learn the chaotic attractor of the competitive Lotka-Volterra model and reproduce histograms of dependent variables, including tails and rare events. We use the Generalized Extreme Value distribution to quantify the tail behavior.

Application of Machine Learning and Convex Limiting to Subgrid Flux Modeling in the Shallow-Water Equations

We propose a combination of machine learning and flux limiting for property-preserving subgrid scale modeling in the context of flux-limited finite volume methods for the one-dimensional shallow-water equations. The numerical fluxes of a conservative target scheme are fitted to the coarse-mesh averages of a monotone fine-grid discretization using a neural network to parametrize the subgrid scale components. To ensure positivity preservation and the validity of local maximum principles, we use a flux limiter that constrains the intermediate states of an equivalent fluctuation form to stay in a convex admissible set. The results of our numerical studies confirm that the proposed combination of machine learning with monolithic convex limiting produces meaningful closures even in scenarios for which the network was not trained.

Predicting Shallow Water Dynamics using Echo-State Networks with Transfer Learning

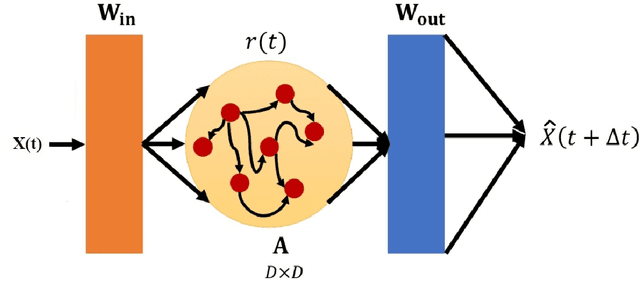
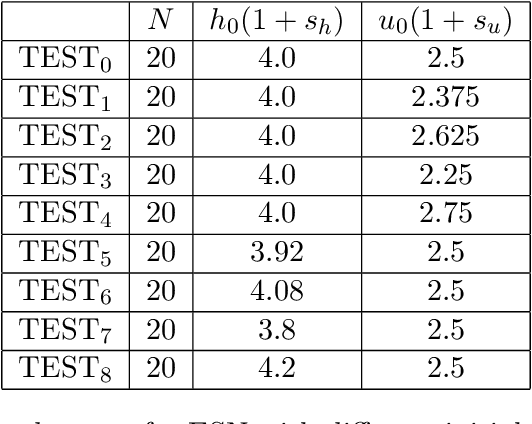
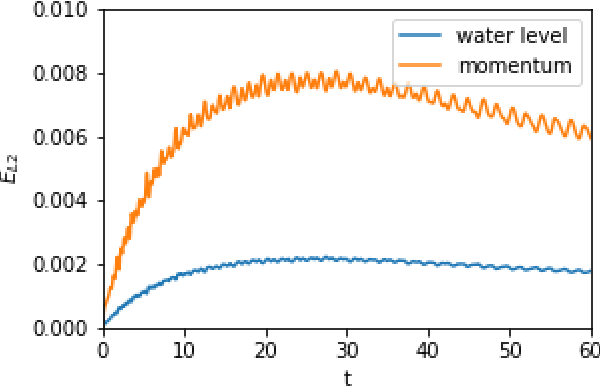
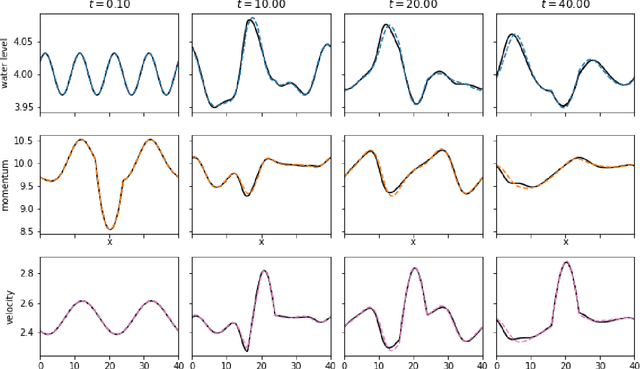
In this paper we demonstrate that reservoir computing can be used to learn the dynamics of the shallow-water equations. In particular, while most previous applications of reservoir computing have required training on a particular trajectory to further predict the evolution along that trajectory alone, we show the capability of reservoir computing to predict trajectories of the shallow-water equations with initial conditions not seen in the training process. However, in this setting, we find that the performance of the network deteriorates for initial conditions with ambient conditions (such as total water height and average velocity) that are different from those in the training dataset. To circumvent this deficiency, we introduce a transfer learning approach wherein a small additional training step with the relevant ambient conditions is used to improve the predictions.