Jimmy Dai
SITCOM: Step-wise Triple-Consistent Diffusion Sampling for Inverse Problems
Oct 06, 2024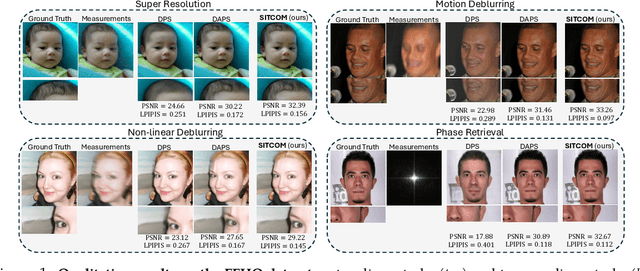
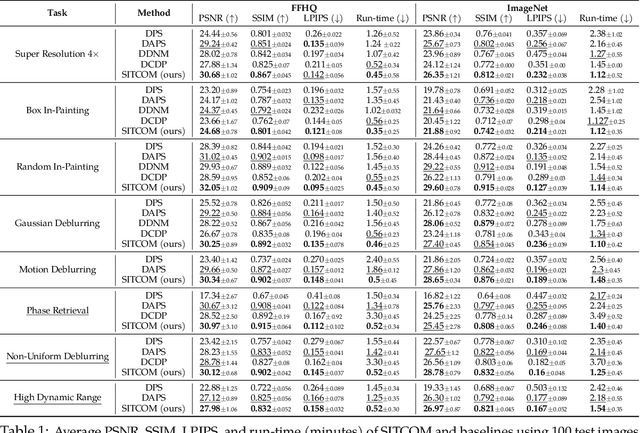

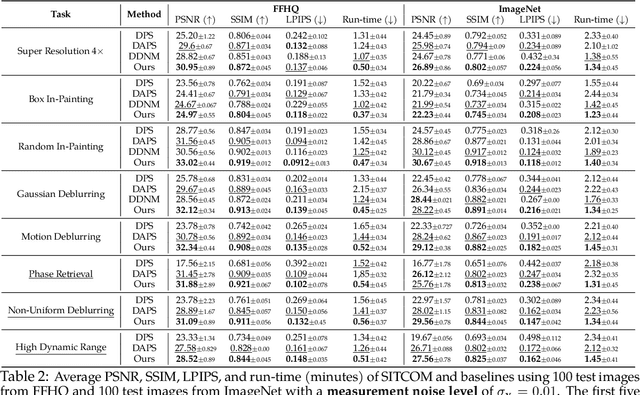
Abstract:Diffusion models (DMs) are a class of generative models that allow sampling from a distribution learned over a training set. When applied to solving inverse imaging problems (IPs), the reverse sampling steps of DMs are typically modified to approximately sample from a measurement-conditioned distribution in the image space. However, these modifications may be unsuitable for certain settings (such as in the presence of measurement noise) and non-linear tasks, as they often struggle to correct errors from earlier sampling steps and generally require a large number of optimization and/or sampling steps. To address these challenges, we state three conditions for achieving measurement-consistent diffusion trajectories. Building on these conditions, we propose a new optimization-based sampling method that not only enforces the standard data manifold measurement consistency and forward diffusion consistency, as seen in previous studies, but also incorporates backward diffusion consistency that maintains a diffusion trajectory by optimizing over the input of the pre-trained model at every sampling step. By enforcing these conditions, either implicitly or explicitly, our sampler requires significantly fewer reverse steps. Therefore, we refer to our accelerated method as Step-wise Triple-Consistent Sampling (SITCOM). Compared to existing state-of-the-art baseline methods, under different levels of measurement noise, our extensive experiments across five linear and three non-linear image restoration tasks demonstrate that SITCOM achieves competitive or superior results in terms of standard image similarity metrics while requiring a significantly reduced run-time across all considered tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge