Handling the Positive-Definite Constraint in the Bayesian Learning Rule

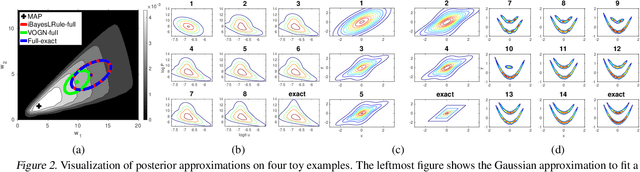
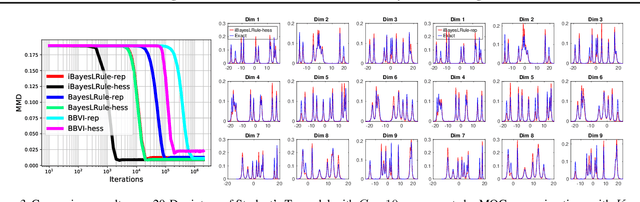
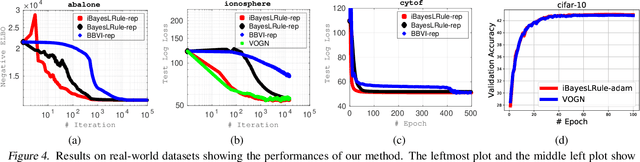
The Bayesian learning rule is a recently proposed variational inference method, which not only contains many existing learning algorithms as special cases but also enables the design of new algorithms. Unfortunately, when posterior parameters lie in an open constraint set, the rule may not satisfy the constraints and requires line-searches which could slow down the algorithm. In this paper, we fix this issue for the positive-definite constraint by proposing an improved rule that naturally handles the constraint. Our modification is obtained using Riemannian gradient methods, and is valid when the approximation attains a \emph{block-coordinate natural parameterization} (e.g., Gaussian distributions and their mixtures). Our method outperforms existing methods without any significant increase in computation. Our work makes it easier to apply the learning rule in the presence of positive-definite constraints in parameter spaces.