ExMAG: Learning of Maximally Ancestral Graphs

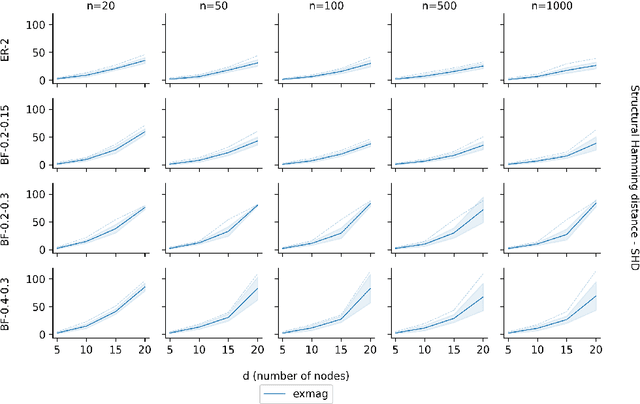
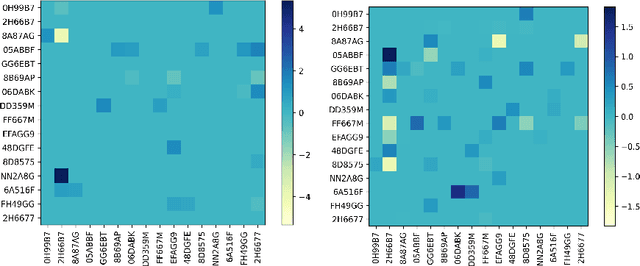
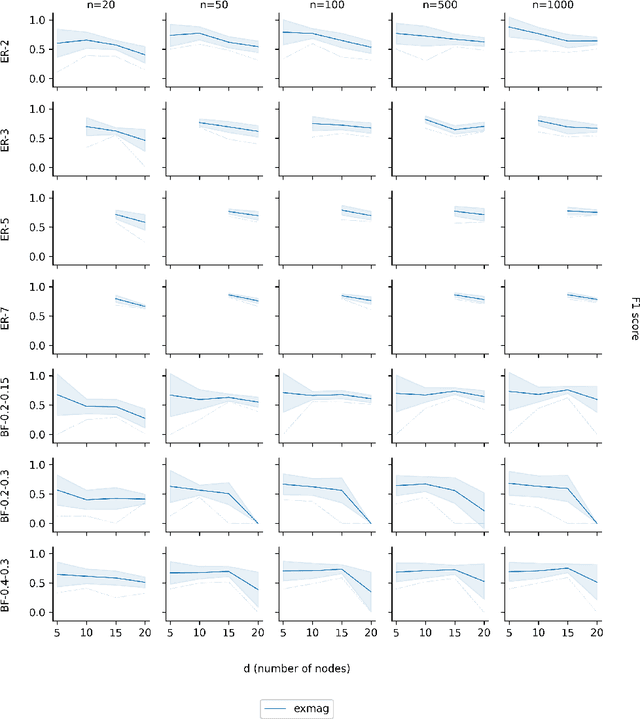
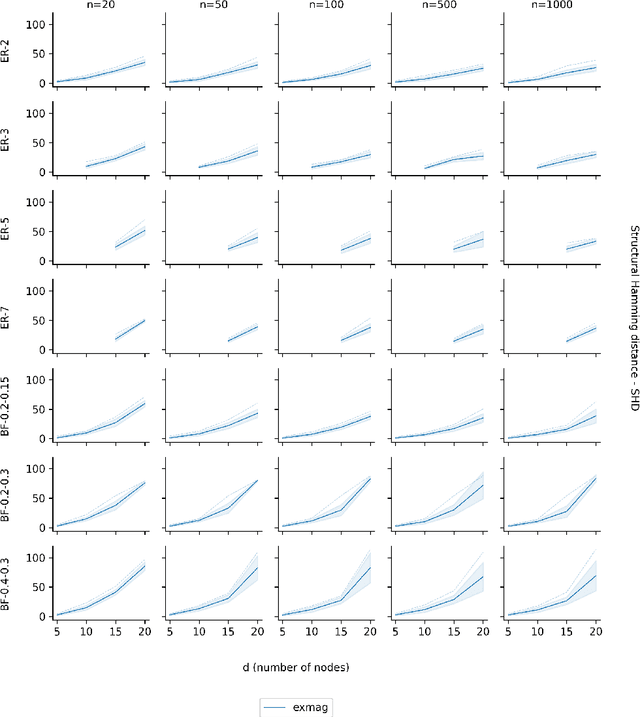
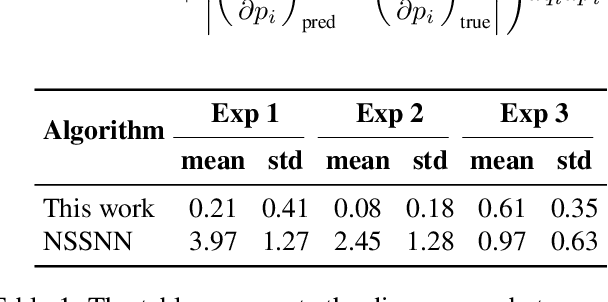
As one transitions from statistical to causal learning, one is seeking the most appropriate causal model. Dynamic Bayesian networks are a popular model, where a weighted directed acyclic graph represents the causal relationships. Stochastic processes are represented by its vertices, and weighted oriented edges suggest the strength of the causal relationships. When there are confounders, one would like to utilize both oriented edges (when the direction of causality is clear) and edges that are not oriented (when there is a confounder), yielding mixed graphs. A little-studied extension of acyclicity to this mixed-graph setting is known as maximally ancestral graphs. We propose a score-based learning algorithm for learning maximally ancestral graphs. A mixed-integer quadratic program is formulated, and an algorithmic approach is proposed, in which the pre-generation of exponentially many constraints is avoided by generating only violated constraints in the so-called branch-and-cut (``lazy constraint'') method. Comparing the novel approach to the state-of-the-art, we show that the proposed approach turns out to produce more accurate results when applied to small and medium-sized synthetic instances containing up to 25 variables.

Federated Sinkhorn

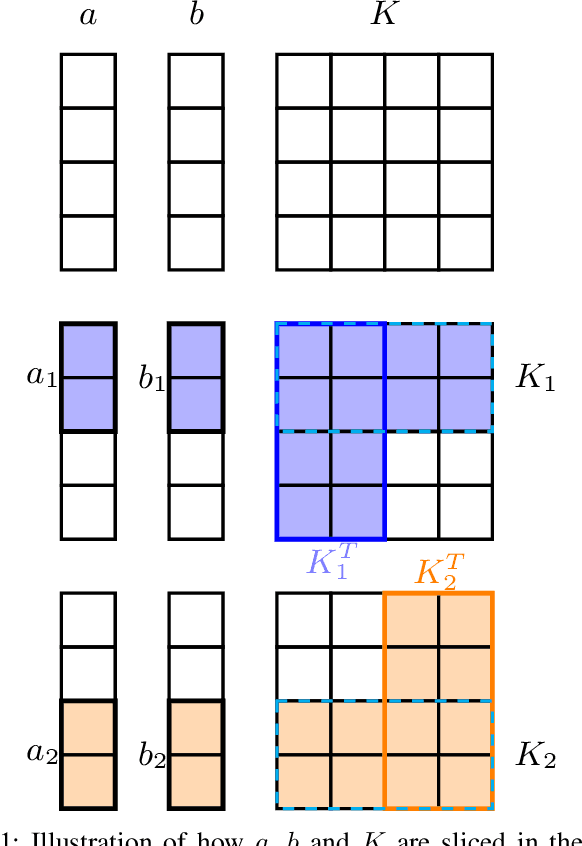
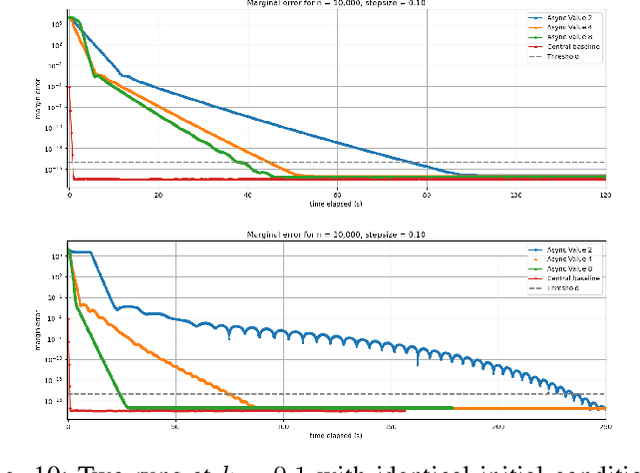
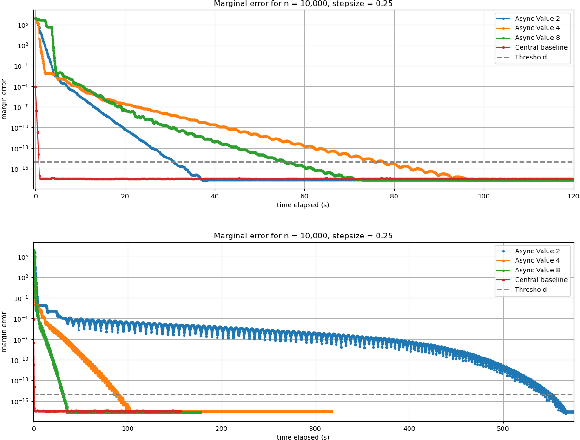
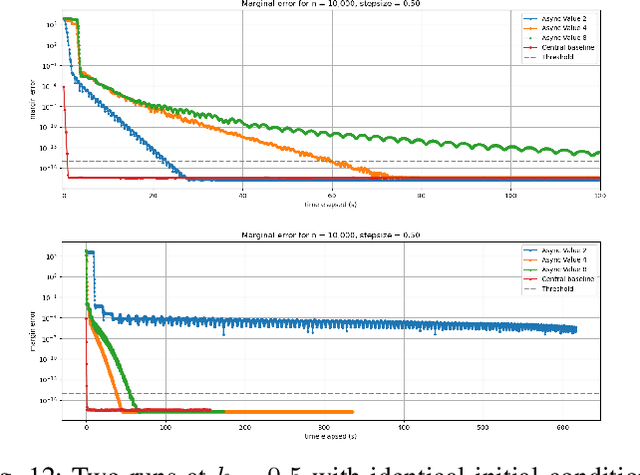
In this work we investigate the potential of solving the discrete Optimal Transport (OT) problem with entropy regularization in a federated learning setting. Recall that the celebrated Sinkhorn algorithm transforms the classical OT linear program into strongly convex constrained optimization, facilitating first order methods for otherwise intractably large problems. A common contemporary setting that remains an open problem as far as the application of Sinkhorn is the presence of data spread across clients with distributed inter-communication, either due to clients whose privacy is a concern, or simply by necessity of processing and memory hardware limitations. In this work we investigate various natural procedures, which we refer to as Federated Sinkhorn, that handle distributed environments where data is partitioned across multiple clients. We formulate the problem as minimizing the transport cost with an entropy regularization term, subject to marginal constraints, where block components of the source and target distribution vectors are locally known to clients corresponding to each block. We consider both synchronous and asynchronous variants as well as all-to-all and server-client communication topology protocols. Each procedure allows clients to compute local operations on their data partition while periodically exchanging information with others. We provide theoretical guarantees on convergence for the different variants under different possible conditions. We empirically demonstrate the algorithms performance on synthetic datasets and a real-world financial risk assessment application. The investigation highlights the subtle tradeoffs associated with computation and communication time in different settings and how they depend on problem size and sparsity.

ExDBN: Exact learning of Dynamic Bayesian Networks

Causal learning from data has received much attention in recent years. One way of capturing causal relationships is by utilizing Bayesian networks. There, one recovers a weighted directed acyclic graph, in which random variables are represented by vertices, and the weights associated with each edge represent the strengths of the causal relationships between them. This concept is extended to capture dynamic effects by introducing a dependency on past data, which may be captured by the structural equation model, which is utilized in the present contribution to formulate a score-based learning approach. A mixed-integer quadratic program is formulated and an algorithmic solution proposed, in which the pre-generation of exponentially many acyclicity constraints is avoided by utilizing the so-called branch-and-cut ("lazy constraint") method. Comparing the novel approach to the state of the art, we show that the proposed approach turns out to produce excellent results when applied to small and medium-sized synthetic instances of up to 25 time-series. Lastly, two interesting applications in bio-science and finance, to which the method is directly applied, further stress the opportunities in developing highly accurate, globally convergent solvers that can handle modest instances.

Learning Generalized Hamiltonians using fully Symplectic Mappings

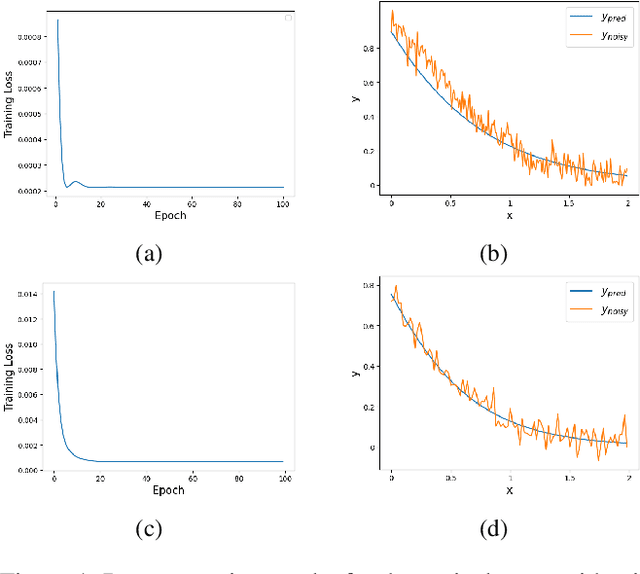
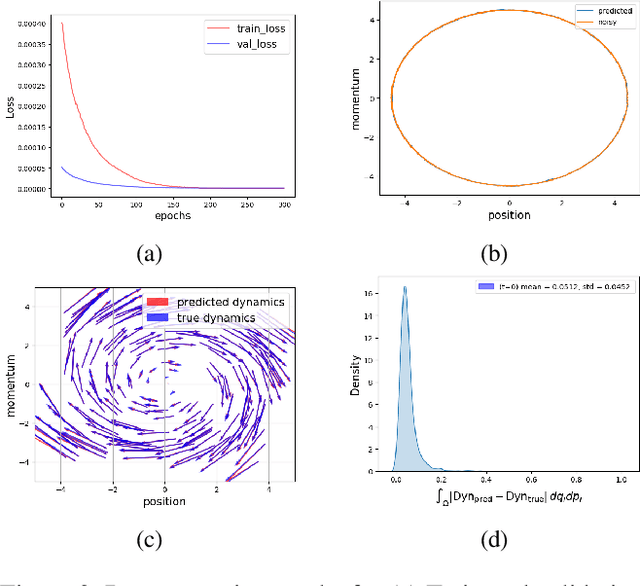
Many important physical systems can be described as the evolution of a Hamiltonian system, which has the important property of being conservative, that is, energy is conserved throughout the evolution. Physics Informed Neural Networks and in particular Hamiltonian Neural Networks have emerged as a mechanism to incorporate structural inductive bias into the NN model. By ensuring physical invariances are conserved, the models exhibit significantly better sample complexity and out-of-distribution accuracy than standard NNs. Learning the Hamiltonian as a function of its canonical variables, typically position and velocity, from sample observations of the system thus becomes a critical task in system identification and long-term prediction of system behavior. However, to truly preserve the long-run physical conservation properties of Hamiltonian systems, one must use symplectic integrators for a forward pass of the system's simulation. While symplectic schemes have been used in the literature, they are thus far limited to situations when they reduce to explicit algorithms, which include the case of separable Hamiltonians or augmented non-separable Hamiltonians. We extend it to generalized non-separable Hamiltonians, and noting the self-adjoint property of symplectic integrators, we bypass computationally intensive backpropagation through an ODE solver. We show that the method is robust to noise and provides a good approximation of the system Hamiltonian when the state variables are sampled from a noisy observation. In the numerical results, we show the performance of the method concerning Hamiltonian reconstruction and conservation, indicating its particular advantage for non-separable systems.

Taming Binarized Neural Networks and Mixed-Integer Programs

There has been a great deal of recent interest in binarized neural networks, especially because of their explainability. At the same time, automatic differentiation algorithms such as backpropagation fail for binarized neural networks, which limits their applicability. By reformulating the problem of training binarized neural networks as a subadditive dual of a mixed-integer program, we show that binarized neural networks admit a tame representation. This, in turn, makes it possible to use the framework of Bolte et al. for implicit differentiation, which offers the possibility for practical implementation of backpropagation in the context of binarized neural networks. This approach could also be used for a broader class of mixed-integer programs, beyond the training of binarized neural networks, as encountered in symbolic approaches to AI and beyond.

Recovering models of open quantum systems from data via polynomial optimization: Towards globally convergent quantum system identification

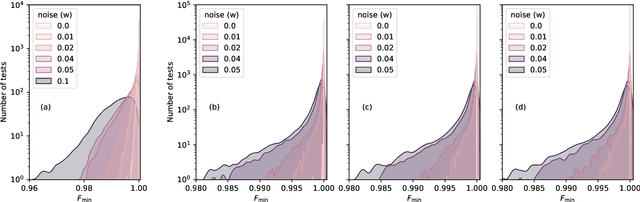
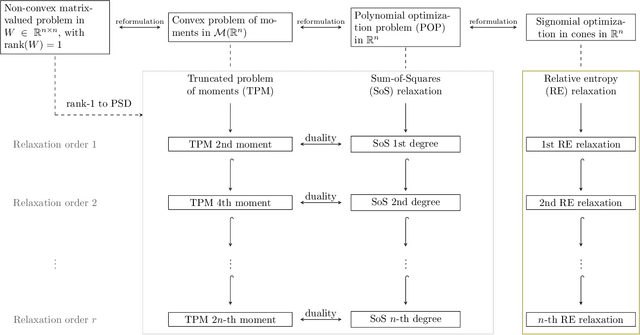
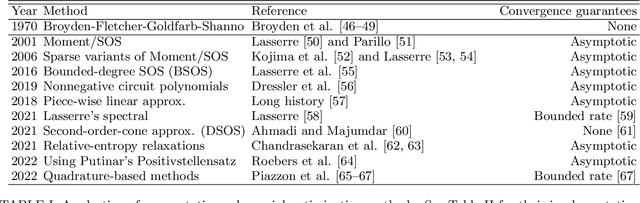
Current quantum devices suffer imperfections as a result of fabrication, as well as noise and dissipation as a result of coupling to their immediate environments. Because of this, it is often difficult to obtain accurate models of their dynamics from first principles. An alternative is to extract such models from time-series measurements of their behavior. Here, we formulate this system-identification problem as a polynomial optimization problem. Recent advances in optimization have provided globally convergent solvers for this class of problems, which using our formulation prove estimates of the Kraus map or the Lindblad equation. We include an overview of the state-of-the-art algorithms, bounds, and convergence rates, and illustrate the use of this approach to modeling open quantum systems.