Zakhar Popovych
Recovering models of open quantum systems from data via polynomial optimization: Towards globally convergent quantum system identification
Mar 31, 2022
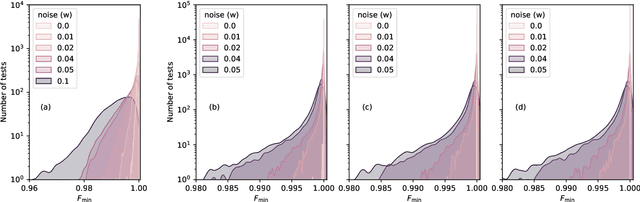
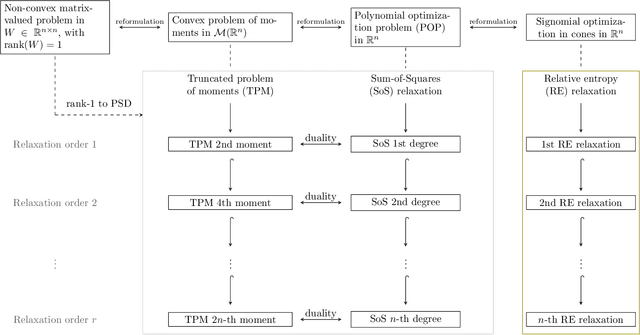
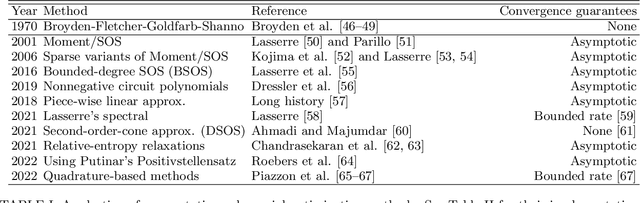
Abstract:Current quantum devices suffer imperfections as a result of fabrication, as well as noise and dissipation as a result of coupling to their immediate environments. Because of this, it is often difficult to obtain accurate models of their dynamics from first principles. An alternative is to extract such models from time-series measurements of their behavior. Here, we formulate this system-identification problem as a polynomial optimization problem. Recent advances in optimization have provided globally convergent solvers for this class of problems, which using our formulation prove estimates of the Kraus map or the Lindblad equation. We include an overview of the state-of-the-art algorithms, bounds, and convergence rates, and illustrate the use of this approach to modeling open quantum systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge