Federated Sinkhorn

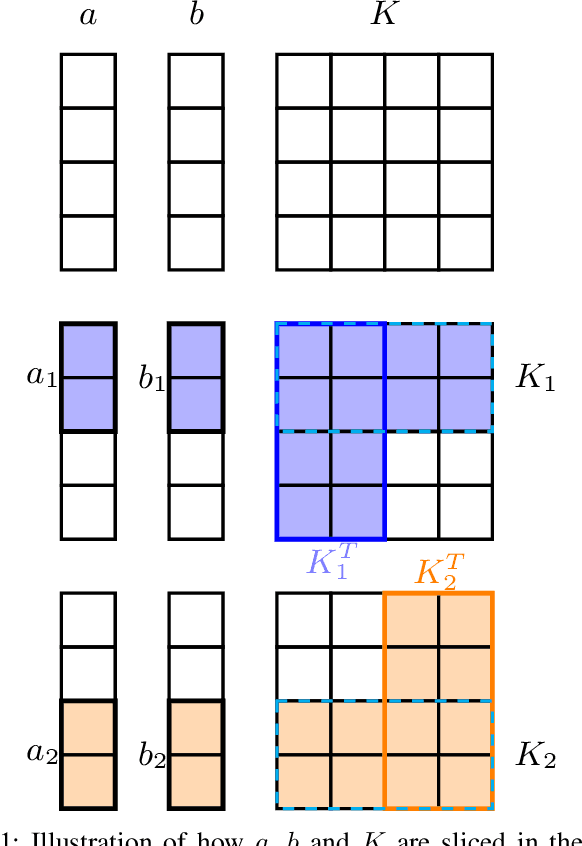
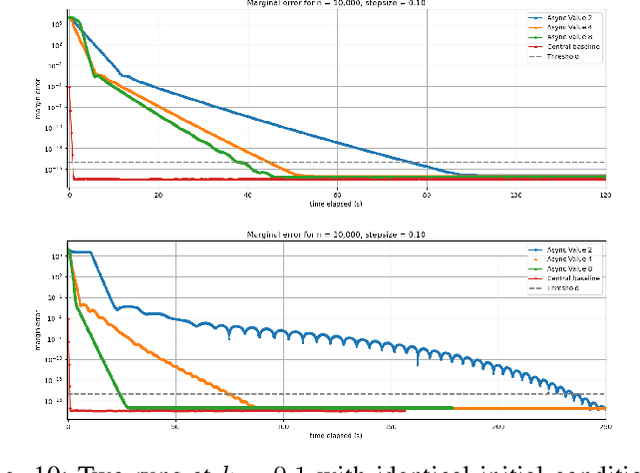
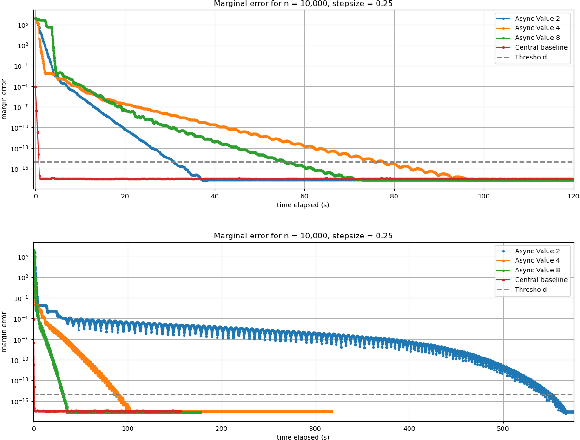
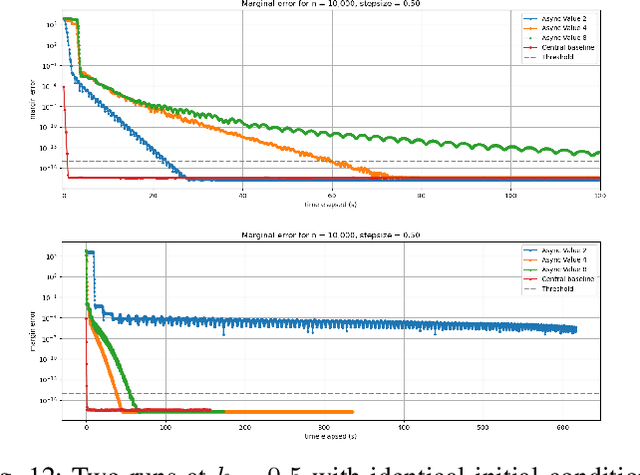
In this work we investigate the potential of solving the discrete Optimal Transport (OT) problem with entropy regularization in a federated learning setting. Recall that the celebrated Sinkhorn algorithm transforms the classical OT linear program into strongly convex constrained optimization, facilitating first order methods for otherwise intractably large problems. A common contemporary setting that remains an open problem as far as the application of Sinkhorn is the presence of data spread across clients with distributed inter-communication, either due to clients whose privacy is a concern, or simply by necessity of processing and memory hardware limitations. In this work we investigate various natural procedures, which we refer to as Federated Sinkhorn, that handle distributed environments where data is partitioned across multiple clients. We formulate the problem as minimizing the transport cost with an entropy regularization term, subject to marginal constraints, where block components of the source and target distribution vectors are locally known to clients corresponding to each block. We consider both synchronous and asynchronous variants as well as all-to-all and server-client communication topology protocols. Each procedure allows clients to compute local operations on their data partition while periodically exchanging information with others. We provide theoretical guarantees on convergence for the different variants under different possible conditions. We empirically demonstrate the algorithms performance on synthetic datasets and a real-world financial risk assessment application. The investigation highlights the subtle tradeoffs associated with computation and communication time in different settings and how they depend on problem size and sparsity.