Low Resource Video Super-resolution using Memory and Residual Deformable Convolutions

Transformer-based video super-resolution (VSR) models have set new benchmarks in recent years, but their substantial computational demands make most of them unsuitable for deployment on resource-constrained devices. Achieving a balance between model complexity and output quality remains a formidable challenge in VSR. Although lightweight models have been introduced to address this issue, they often struggle to deliver state-of-the-art performance. We propose a novel lightweight, parameter-efficient deep residual deformable convolution network for VSR. Unlike prior methods, our model enhances feature utilization through residual connections and employs deformable convolution for precise frame alignment, addressing motion dynamics effectively. Furthermore, we introduce a single memory tensor to capture information accrued from the past frames and improve motion estimation across frames. This design enables an efficient balance between computational cost and reconstruction quality. With just 2.3 million parameters, our model achieves state-of-the-art SSIM of 0.9175 on the REDS4 dataset, surpassing existing lightweight and many heavy models in both accuracy and resource efficiency. Architectural insights from our model pave the way for real-time VSR on streaming data.

Learning Generalized Hamiltonians using fully Symplectic Mappings

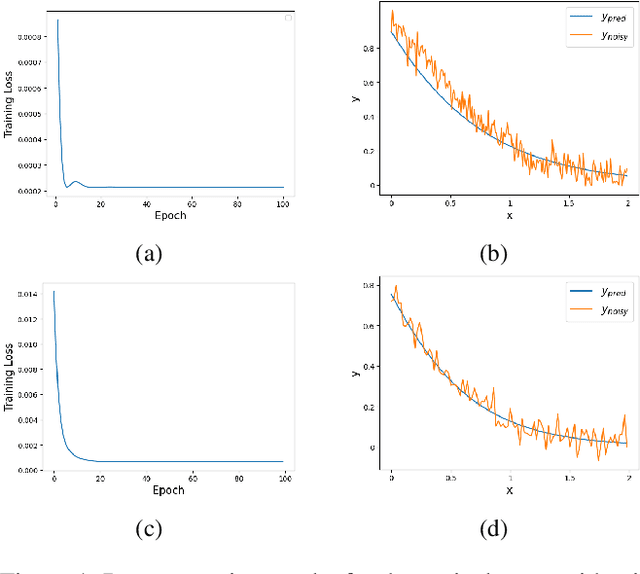
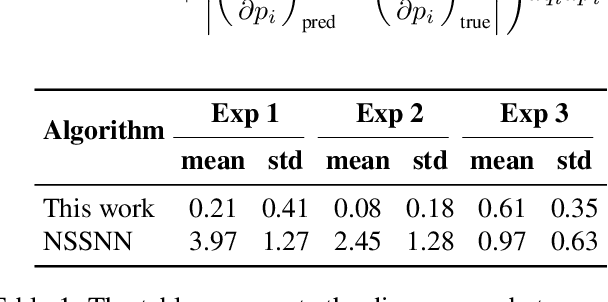
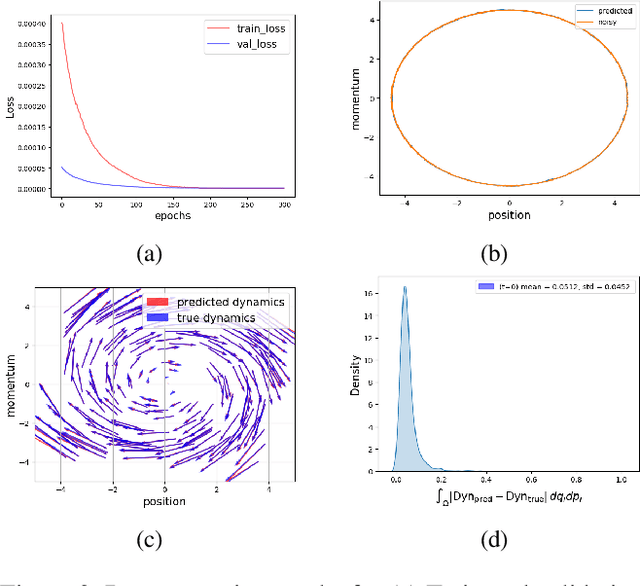
Many important physical systems can be described as the evolution of a Hamiltonian system, which has the important property of being conservative, that is, energy is conserved throughout the evolution. Physics Informed Neural Networks and in particular Hamiltonian Neural Networks have emerged as a mechanism to incorporate structural inductive bias into the NN model. By ensuring physical invariances are conserved, the models exhibit significantly better sample complexity and out-of-distribution accuracy than standard NNs. Learning the Hamiltonian as a function of its canonical variables, typically position and velocity, from sample observations of the system thus becomes a critical task in system identification and long-term prediction of system behavior. However, to truly preserve the long-run physical conservation properties of Hamiltonian systems, one must use symplectic integrators for a forward pass of the system's simulation. While symplectic schemes have been used in the literature, they are thus far limited to situations when they reduce to explicit algorithms, which include the case of separable Hamiltonians or augmented non-separable Hamiltonians. We extend it to generalized non-separable Hamiltonians, and noting the self-adjoint property of symplectic integrators, we bypass computationally intensive backpropagation through an ODE solver. We show that the method is robust to noise and provides a good approximation of the system Hamiltonian when the state variables are sampled from a noisy observation. In the numerical results, we show the performance of the method concerning Hamiltonian reconstruction and conservation, indicating its particular advantage for non-separable systems.