Koopman Operators in Robot Learning

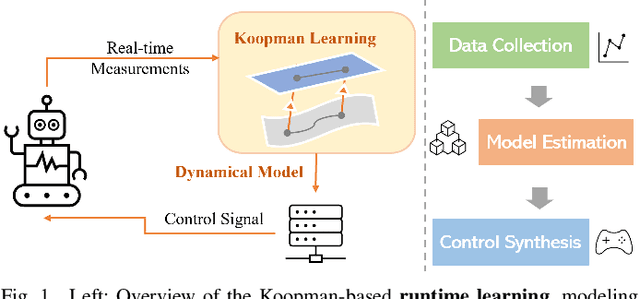
Koopman operator theory offers a rigorous treatment of dynamics and has been emerging as a powerful modeling and learning-based control method enabling significant advancements across various domains of robotics. Due to its ability to represent nonlinear dynamics as a linear operator, Koopman theory offers a fresh lens through which to understand and tackle the modeling and control of complex robotic systems. Moreover, it enables incremental updates and is computationally inexpensive making it particularly appealing for real-time applications and online active learning. This review comprehensively presents recent research results on advancing Koopman operator theory across diverse domains of robotics, encompassing aerial, legged, wheeled, underwater, soft, and manipulator robotics. Furthermore, it offers practical tutorials to help new users get started as well as a treatise of more advanced topics leading to an outlook on future directions and open research questions. Taken together, these provide insights into the potential evolution of Koopman theory as applied to the field of robotics.

Temporal Forward-Backward Consistency, Not Residual Error, Measures the Prediction Accuracy of Extended Dynamic Mode Decomposition

Extended Dynamic Mode Decomposition (EDMD) is a popular data-driven method to approximate the action of the Koopman operator on a linear function space spanned by a dictionary of functions. The accuracy of EDMD model critically depends on the quality of the particular dictionary's span, specifically on how close it is to being invariant under the Koopman operator. Motivated by the observation that the residual error of EDMD, typically used for dictionary learning, does not encode the quality of the function space and is sensitive to the choice of basis, we introduce the novel concept of consistency index. We show that this measure, based on using EDMD forward and backward in time, enjoys a number of desirable qualities that make it suitable for data-driven modeling of dynamical systems: it measures the quality of the function space, it is invariant under the choice of basis, can be computed in closed form from the data, and provides a tight upper-bound for the relative root mean square error of all function predictions on the entire span of the dictionary.

Generalizing Dynamic Mode Decomposition: Balancing Accuracy and Expressiveness in Koopman Approximations

This paper tackles the data-driven approximation of unknown dynamical systems using Koopman-operator methods. Given a dictionary of functions, these methods approximate the projection of the action of the operator on the finite-dimensional subspace spanned by the dictionary. We propose the Tunable Symmetric Subspace Decomposition algorithm to refine the dictionary, balancing its expressiveness and accuracy. Expressiveness corresponds to the ability of the dictionary to describe the evolution of as many observables as possible and accuracy corresponds to the ability to correctly predict their evolution. Based on the observation that Koopman-invariant subspaces give rise to exact predictions, we reason that prediction accuracy is a function of the degree of invariance of the subspace generated by the dictionary and provide a data-driven measure to measure invariance proximity. The proposed algorithm iteratively prunes the initial functional space to identify a refined dictionary of functions that satisfies the desired level of accuracy while retaining as much of the original expressiveness as possible. We provide a full characterization of the algorithm properties and show that it generalizes both Extended Dynamic Mode Decomposition and Symmetric Subspace Decomposition. Simulations on planar systems show the effectiveness of the proposed methods in producing Koopman approximations of tunable accuracy that capture relevant information about the dynamical system.