Surveying the space of descriptions of a composite system with machine learning

Multivariate information theory provides a general and principled framework for understanding how the components of a complex system are connected. Existing analyses are coarse in nature -- built up from characterizations of discrete subsystems -- and can be computationally prohibitive. In this work, we propose to study the continuous space of possible descriptions of a composite system as a window into its organizational structure. A description consists of specific information conveyed about each of the components, and the space of possible descriptions is equivalent to the space of lossy compression schemes of the components. We introduce a machine learning framework to optimize descriptions that extremize key information theoretic quantities used to characterize organization, such as total correlation and O-information. Through case studies on spin systems, Sudoku boards, and letter sequences from natural language, we identify extremal descriptions that reveal how system-wide variation emerges from individual components. By integrating machine learning into a fine-grained information theoretic analysis of composite random variables, our framework opens a new avenues for probing the structure of real-world complex systems.

Which bits went where? Past and future transfer entropy decomposition with the information bottleneck

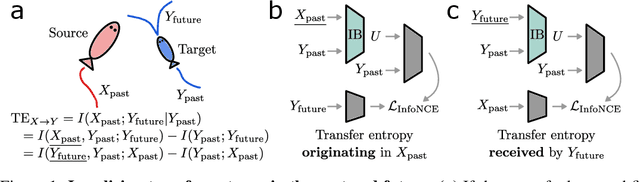
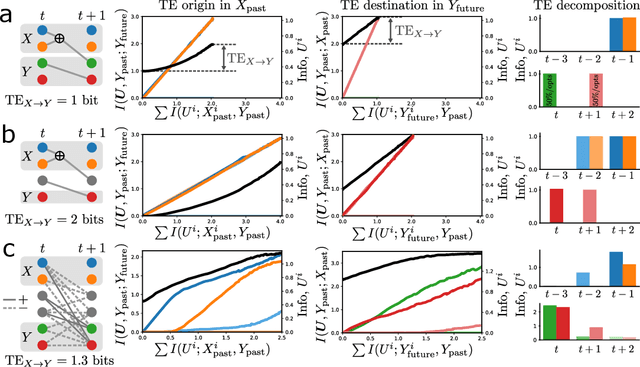
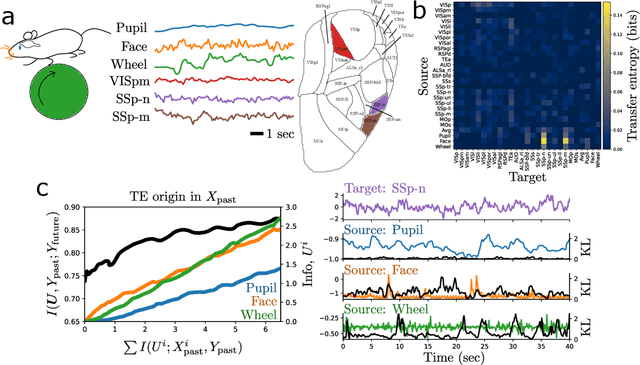
Whether the system under study is a shoal of fish, a collection of neurons, or a set of interacting atmospheric and oceanic processes, transfer entropy measures the flow of information between time series and can detect possible causal relationships. Much like mutual information, transfer entropy is generally reported as a single value summarizing an amount of shared variation, yet a more fine-grained accounting might illuminate much about the processes under study. Here we propose to decompose transfer entropy and localize the bits of variation on both sides of information flow: that of the originating process's past and that of the receiving process's future. We employ the information bottleneck (IB) to compress the time series and identify the transferred entropy. We apply our method to decompose the transfer entropy in several synthetic recurrent processes and an experimental mouse dataset of concurrent behavioral and neural activity. Our approach highlights the nuanced dynamics within information flow, laying a foundation for future explorations into the intricate interplay of temporal processes in complex systems.

Comparing information content of representation spaces for disentanglement with VAE ensembles

Disentanglement is the endeavour to use machine learning to divide information about a dataset into meaningful fragments. In practice these fragments are representation (sub)spaces, often the set of channels in the latent space of a variational autoencoder (VAE). Assessments of disentanglement predominantly employ metrics that are coarse-grained at the model level, but this approach can obscure much about the process of information fragmentation. Here we propose to study the learned channels in aggregate, as the fragments of information learned by an ensemble of repeat training runs. Additionally, we depart from prior work where measures of similarity between individual subspaces neglected the nature of data embeddings as probability distributions. Instead, we view representation subspaces as communication channels that perform a soft clustering of the data; consequently, we generalize two classic information-theoretic measures of similarity between clustering assignments to compare representation spaces. We develop a lightweight method of estimation based on fingerprinting representation subspaces by their ability to distinguish dataset samples, allowing us to identify, analyze, and leverage meaningful structure in ensembles of VAEs trained on synthetic and natural datasets. Using this fully unsupervised pipeline we identify "hotspots" in the space of information fragments: groups of nearly identical representation subspaces that appear repeatedly in an ensemble of VAEs, particularly as regularization is increased. Finally, we leverage the proposed methodology to achieve ensemble learning with VAEs, boosting the information content of a set of weak learners -- a capability not possible with previous methods of assessing channel similarity.

Optimized measurements of chaotic dynamical systems via the information bottleneck

Deterministic chaos permits a precise notion of a "perfect measurement" as one that, when obtained repeatedly, captures all of the information created by the system's evolution with minimal redundancy. Finding an optimal measurement is challenging, and has generally required intimate knowledge of the dynamics in the few cases where it has been done. We establish an equivalence between a perfect measurement and a variant of the information bottleneck. As a consequence, we can employ machine learning to optimize measurement processes that efficiently extract information from trajectory data. We obtain approximately optimal measurements for multiple chaotic maps and lay the necessary groundwork for efficient information extraction from general time series.

Intrinsically motivated graph exploration using network theories of human curiosity

Intrinsically motivated exploration has proven useful for reinforcement learning, even without additional extrinsic rewards. When the environment is naturally represented as a graph, how to guide exploration best remains an open question. In this work, we propose a novel approach for exploring graph-structured data motivated by two theories of human curiosity: the information gap theory and the compression progress theory. The theories view curiosity as an intrinsic motivation to optimize for topological features of subgraphs induced by the visited nodes in the environment. We use these proposed features as rewards for graph neural-network-based reinforcement learning. On multiple classes of synthetically generated graphs, we find that trained agents generalize to larger environments and to longer exploratory walks than are seen during training. Our method computes more efficiently than the greedy evaluation of the relevant topological properties. The proposed intrinsic motivations bear particular relevance for recommender systems. We demonstrate that curiosity-based recommendations are more predictive of human behavior than PageRank centrality for several real-world graph datasets, including MovieLens, Amazon Books, and Wikispeedia.

Information decomposition to identify relevant variation in complex systems with machine learning

One of the fundamental steps toward understanding a complex system is identifying variation at the scale of the system's components that is most relevant to behavior on a macroscopic scale. Mutual information is a natural means of linking variation across scales of a system due to its independence of the particular functional relationship between variables. However, estimating mutual information given high-dimensional, continuous-valued data is notoriously difficult, and the desideratum -- to reveal important variation in a comprehensible manner -- is only readily achieved through exhaustive search. Here we propose a practical, efficient, and broadly applicable methodology to decompose the information contained in a set of measurements by lossily compressing each measurement with machine learning. Guided by the distributed information bottleneck as a learning objective, the information decomposition sorts variation in the measurements of the system state by relevance to specified macroscale behavior, revealing the most important subsets of measurements for different amounts of predictive information. Additional granularity is achieved by inspection of the learned compression schemes: the variation transmitted during compression is composed of distinctions among measurement values that are most relevant to the macroscale behavior. We focus our analysis on two paradigmatic complex systems: a Boolean circuit and an amorphous material undergoing plastic deformation. In both examples, specific bits of entropy are identified out of the high entropy of the system state as most related to macroscale behavior for insight about the connection between micro- and macro- in the complex system. The identification of meaningful variation in data, with the full generality brought by information theory, is made practical for the study of complex systems.

Interpretability with full complexity by constraining feature information

Interpretability is a pressing issue for machine learning. Common approaches to interpretable machine learning constrain interactions between features of the input, rendering the effects of those features on a model's output comprehensible but at the expense of model complexity. We approach interpretability from a new angle: constrain the information about the features without restricting the complexity of the model. Borrowing from information theory, we use the Distributed Information Bottleneck to find optimal compressions of each feature that maximally preserve information about the output. The learned information allocation, by feature and by feature value, provides rich opportunities for interpretation, particularly in problems with many features and complex feature interactions. The central object of analysis is not a single trained model, but rather a spectrum of models serving as approximations that leverage variable amounts of information about the inputs. Information is allocated to features by their relevance to the output, thereby solving the problem of feature selection by constructing a learned continuum of feature inclusion-to-exclusion. The optimal compression of each feature -- at every stage of approximation -- allows fine-grained inspection of the distinctions among feature values that are most impactful for prediction. We develop a framework for extracting insight from the spectrum of approximate models and demonstrate its utility on a range of tabular datasets.

Characterizing information loss in a chaotic double pendulum with the Information Bottleneck

A hallmark of chaotic dynamics is the loss of information with time. Although information loss is often expressed through a connection to Lyapunov exponents -- valid in the limit of high information about the system state -- this picture misses the rich spectrum of information decay across different levels of granularity. Here we show how machine learning presents new opportunities for the study of information loss in chaotic dynamics, with a double pendulum serving as a model system. We use the Information Bottleneck as a training objective for a neural network to extract information from the state of the system that is optimally predictive of the future state after a prescribed time horizon. We then decompose the optimally predictive information by distributing a bottleneck to each state variable, recovering the relative importance of the variables in determining future evolution. The framework we develop is broadly applicable to chaotic systems and pragmatic to apply, leveraging data and machine learning to monitor the limits of predictability and map out the loss of information.

The Distributed Information Bottleneck reveals the explanatory structure of complex systems

The fruits of science are relationships made comprehensible, often by way of approximation. While deep learning is an extremely powerful way to find relationships in data, its use in science has been hindered by the difficulty of understanding the learned relationships. The Information Bottleneck (IB) is an information theoretic framework for understanding a relationship between an input and an output in terms of a trade-off between the fidelity and complexity of approximations to the relationship. Here we show that a crucial modification -- distributing bottlenecks across multiple components of the input -- opens fundamentally new avenues for interpretable deep learning in science. The Distributed Information Bottleneck throttles the downstream complexity of interactions between the components of the input, deconstructing a relationship into meaningful approximations found through deep learning without requiring custom-made datasets or neural network architectures. Applied to a complex system, the approximations illuminate aspects of the system's nature by restricting -- and monitoring -- the information about different components incorporated into the approximation. We demonstrate the Distributed IB's explanatory utility in systems drawn from applied mathematics and condensed matter physics. In the former, we deconstruct a Boolean circuit into approximations that isolate the most informative subsets of input components without requiring exhaustive search. In the latter, we localize information about future plastic rearrangement in the static structure of a sheared glass, and find the information to be more or less diffuse depending on the system's preparation. By way of a principled scheme of approximations, the Distributed IB brings much-needed interpretability to deep learning and enables unprecedented analysis of information flow through a system.

Learning Continuous Chaotic Attractors with a Reservoir Computer

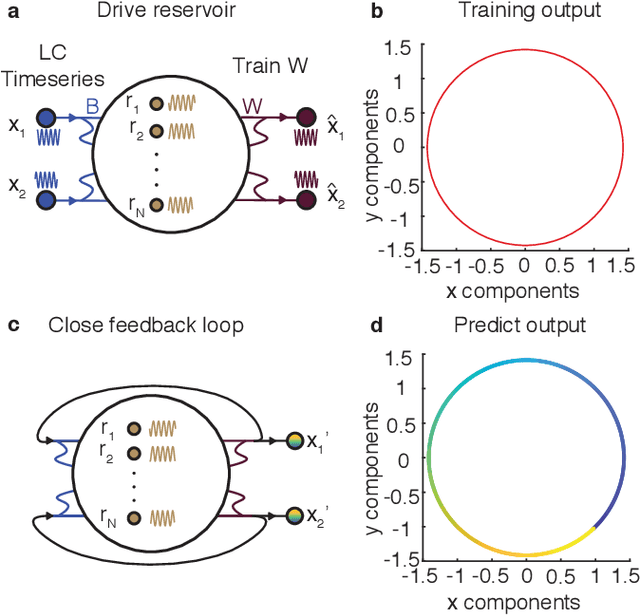
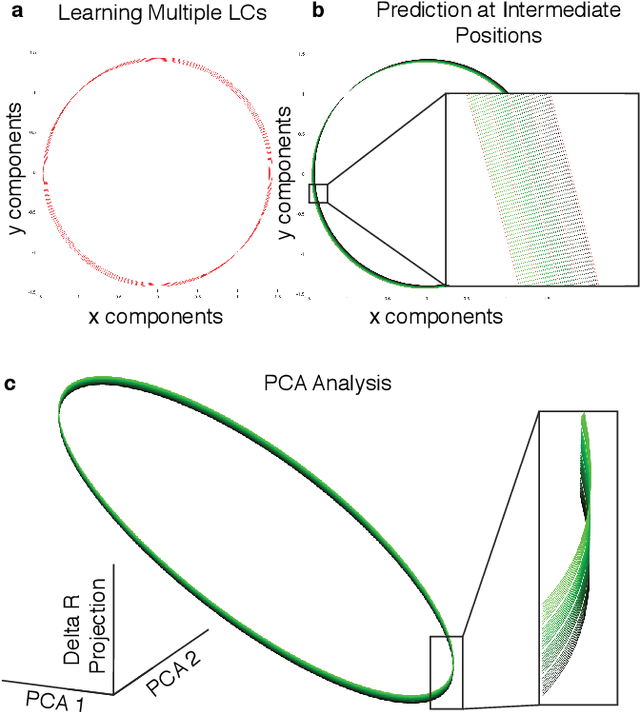
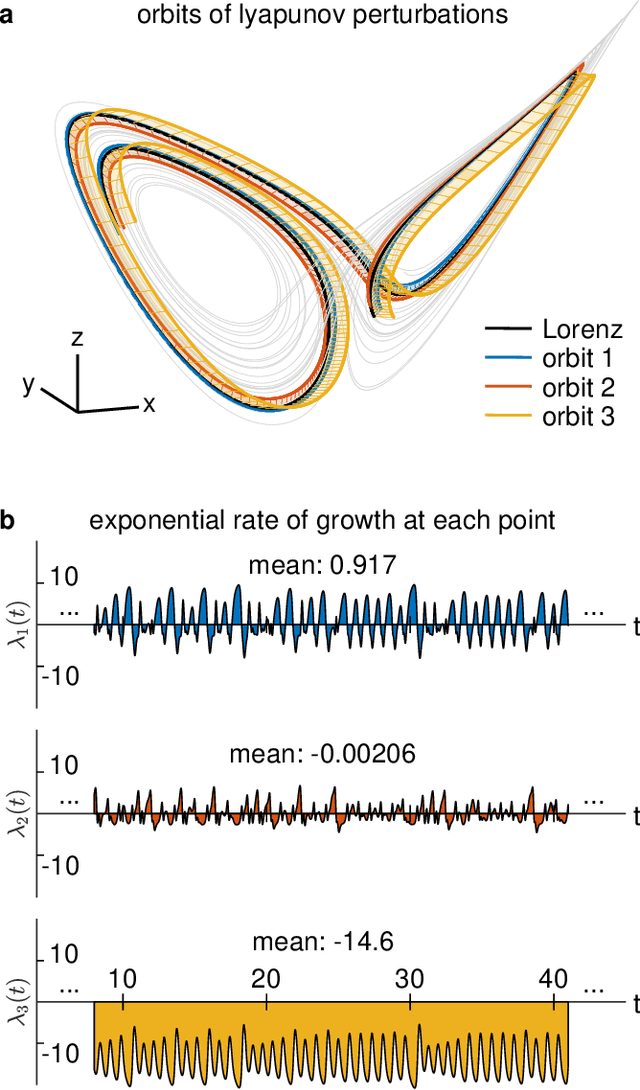
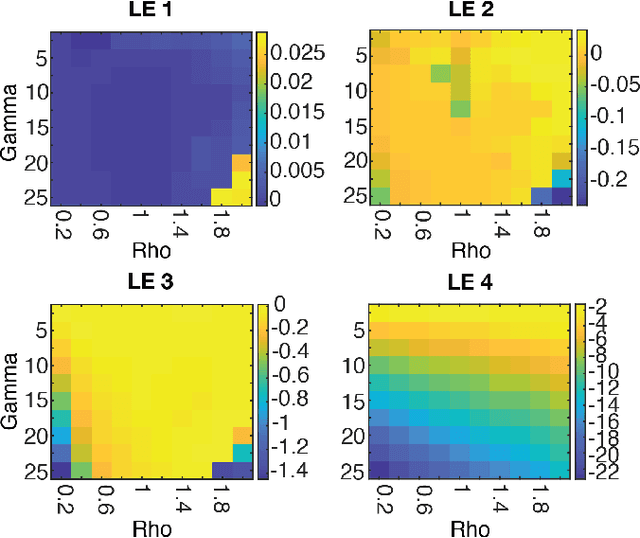
Neural systems are well known for their ability to learn and store information as memories. Even more impressive is their ability to abstract these memories to create complex internal representations, enabling advanced functions such as the spatial manipulation of mental representations. While recurrent neural networks (RNNs) are capable of representing complex information, the exact mechanisms of how dynamical neural systems perform abstraction are still not well-understood, thereby hindering the development of more advanced functions. Here, we train a 1000-neuron RNN -- a reservoir computer (RC) -- to abstract a continuous dynamical attractor memory from isolated examples of dynamical attractor memories. Further, we explain the abstraction mechanism with new theory. By training the RC on isolated and shifted examples of either stable limit cycles or chaotic Lorenz attractors, the RC learns a continuum of attractors, as quantified by an extra Lyapunov exponent equal to zero. We propose a theoretical mechanism of this abstraction by combining ideas from differentiable generalized synchronization and feedback dynamics. Our results quantify abstraction in simple neural systems, enabling us to design artificial RNNs for abstraction, and leading us towards a neural basis of abstraction.