How Initial Connectivity Shapes Biologically Plausible Learning in Recurrent Neural Networks

The impact of initial connectivity on learning has been extensively studied in the context of backpropagation-based gradient descent, but it remains largely underexplored in biologically plausible learning settings. Focusing on recurrent neural networks (RNNs), we found that the initial weight magnitude significantly influences the learning performance of biologically plausible learning rules in a similar manner to its previously observed effect on training via backpropagation through time (BPTT). By examining the maximum Lyapunov exponent before and after training, we uncovered the greater demands that certain initialization schemes place on training to achieve desired information propagation properties. Consequently, we extended the recently proposed gradient flossing method, which regularizes the Lyapunov exponents, to biologically plausible learning and observed an improvement in learning performance. To our knowledge, we are the first to examine the impact of initialization on biologically plausible learning rules for RNNs and to subsequently propose a biologically plausible remedy. Such an investigation could lead to predictions about the influence of initial connectivity on learning dynamics and performance, as well as guide neuromorphic design.

Evolutionary algorithms as an alternative to backpropagation for supervised training of Biophysical Neural Networks and Neural ODEs

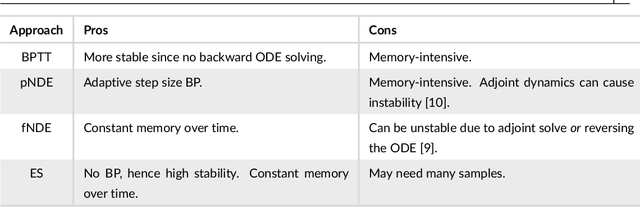
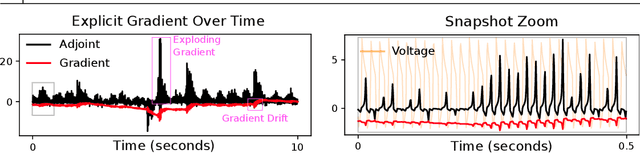
Training networks consisting of biophysically accurate neuron models could allow for new insights into how brain circuits can organize and solve tasks. We begin by analyzing the extent to which the central algorithm for neural network learning -- stochastic gradient descent through backpropagation (BP) -- can be used to train such networks. We find that properties of biophysically based neural network models needed for accurate modelling such as stiffness, high nonlinearity and long evaluation timeframes relative to spike times makes BP unstable and divergent in a variety of cases. To address these instabilities and inspired by recent work, we investigate the use of "gradient-estimating" evolutionary algorithms (EAs) for training biophysically based neural networks. We find that EAs have several advantages making them desirable over direct BP, including being forward-pass only, robust to noisy and rigid losses, allowing for discrete loss formulations, and potentially facilitating a more global exploration of parameters. We apply our method to train a recurrent network of Morris-Lecar neuron models on a stimulus integration and working memory task, and show how it can succeed in cases where direct BP is inapplicable. To expand on the viability of EAs in general, we apply them to a general neural ODE problem and a stiff neural ODE benchmark and find again that EAs can out-perform direct BP here, especially for the over-parameterized regime. Our findings suggest that biophysical neurons could provide useful benchmarks for testing the limits of BP-adjacent methods, and demonstrate the viability of EAs for training networks with complex components.

How connectivity structure shapes rich and lazy learning in neural circuits

In theoretical neuroscience, recent work leverages deep learning tools to explore how some network attributes critically influence its learning dynamics. Notably, initial weight distributions with small (resp. large) variance may yield a rich (resp. lazy) regime, where significant (resp. minor) changes to network states and representation are observed over the course of learning. However, in biology, neural circuit connectivity generally has a low-rank structure and therefore differs markedly from the random initializations generally used for these studies. As such, here we investigate how the structure of the initial weights, in particular their effective rank, influences the network learning regime. Through both empirical and theoretical analyses, we discover that high-rank initializations typically yield smaller network changes indicative of lazier learning, a finding we also confirm with experimentally-driven initial connectivity in recurrent neural networks. Conversely, low-rank initialization biases learning towards richer learning. Importantly, however, as an exception to this rule, we find lazier learning can still occur with a low-rank initialization that aligns with task and data statistics. Our research highlights the pivotal role of initial weight structures in shaping learning regimes, with implications for metabolic costs of plasticity and risks of catastrophic forgetting.

Biologically-plausible backpropagation through arbitrary timespans via local neuromodulators

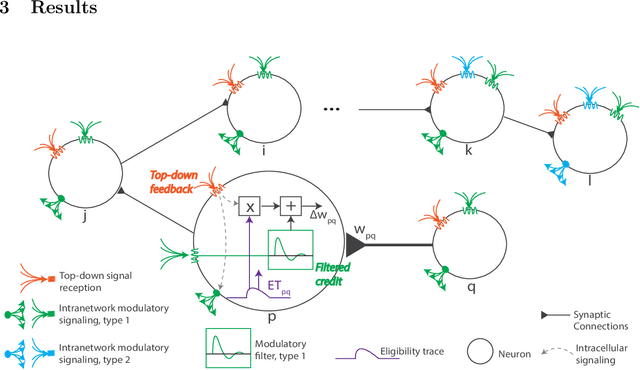
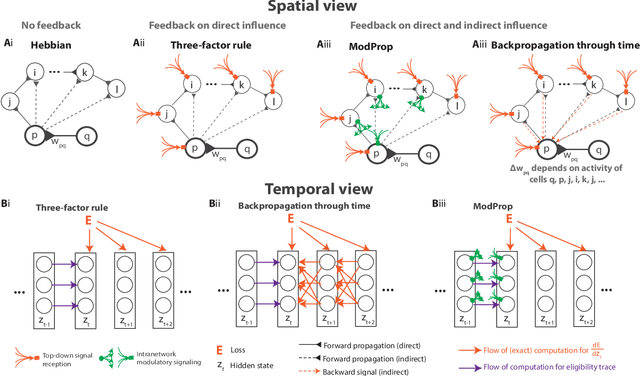
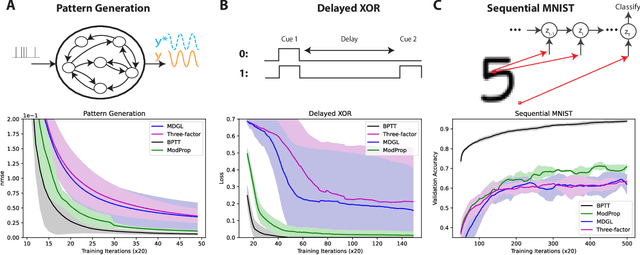
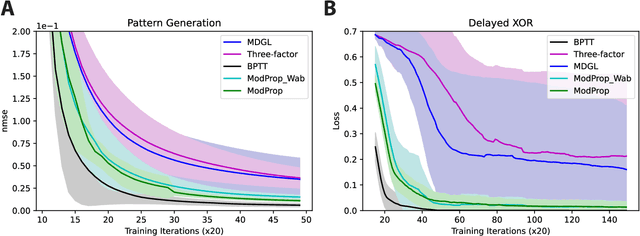
The spectacular successes of recurrent neural network models where key parameters are adjusted via backpropagation-based gradient descent have inspired much thought as to how biological neuronal networks might solve the corresponding synaptic credit assignment problem. There is so far little agreement, however, as to how biological networks could implement the necessary backpropagation through time, given widely recognized constraints of biological synaptic network signaling architectures. Here, we propose that extra-synaptic diffusion of local neuromodulators such as neuropeptides may afford an effective mode of backpropagation lying within the bounds of biological plausibility. Going beyond existing temporal truncation-based gradient approximations, our approximate gradient-based update rule, ModProp, propagates credit information through arbitrary time steps. ModProp suggests that modulatory signals can act on receiving cells by convolving their eligibility traces via causal, time-invariant and synapse-type-specific filter taps. Our mathematical analysis of ModProp learning, together with simulation results on benchmark temporal tasks, demonstrate the advantage of ModProp over existing biologically-plausible temporal credit assignment rules. These results suggest a potential neuronal mechanism for signaling credit information related to recurrent interactions over a longer time horizon. Finally, we derive an in-silico implementation of ModProp that could serve as a low-complexity and causal alternative to backpropagation through time.

Beyond accuracy: generalization properties of bio-plausible temporal credit assignment rules

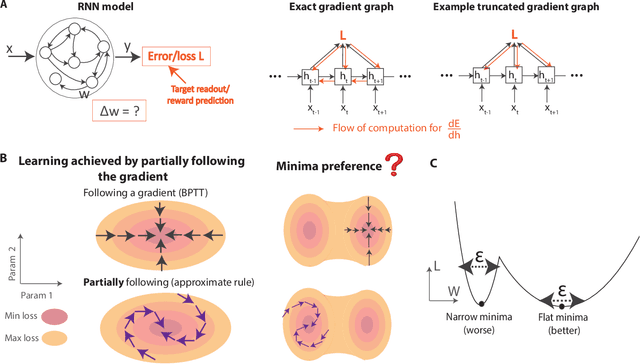
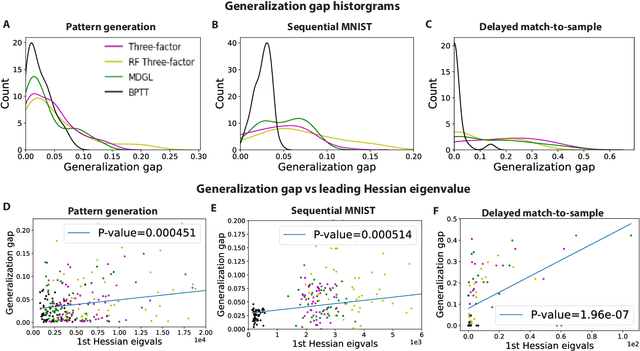
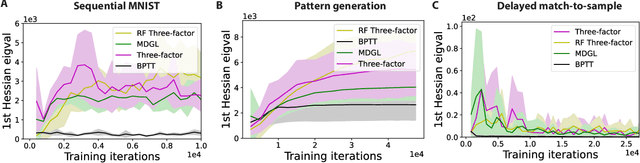
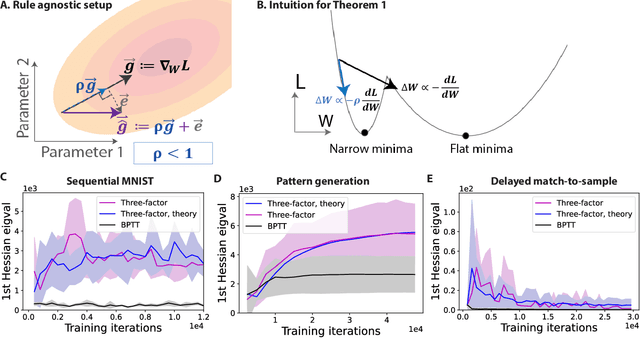
To unveil how the brain learns, ongoing work seeks biologically-plausible approximations of gradient descent algorithms for training recurrent neural networks (RNNs). Yet, beyond task accuracy, it is unclear if such learning rules converge to solutions that exhibit different levels of generalization than their nonbiologically-plausible counterparts. Leveraging results from deep learning theory based on loss landscape curvature, we ask: how do biologically-plausible gradient approximations affect generalization? We first demonstrate that state-of-the-art biologically-plausible learning rules for training RNNs exhibit worse and more variable generalization performance compared to their machine learning counterparts that follow the true gradient more closely. Next, we verify that such generalization performance is correlated significantly with loss landscape curvature, and we show that biologically-plausible learning rules tend to approach high-curvature regions in synaptic weight space. Using tools from dynamical systems, we derive theoretical arguments and present a theorem explaining this phenomenon. This predicts our numerical results, and explains why biologically-plausible rules lead to worse and more variable generalization properties. Finally, we suggest potential remedies that could be used by the brain to mitigate this effect. To our knowledge, our analysis is the first to identify the reason for this generalization gap between artificial and biologically-plausible learning rules, which can help guide future investigations into how the brain learns solutions that generalize.