Flexible inference of learning rules from de novo learning data using neural networks

Understanding how animals learn is a central challenge in neuroscience, with growing relevance to the development of animal- or human-aligned artificial intelligence. However, most existing approaches assume specific parametric forms for the learning rule (e.g., Q-learning, policy gradient) or are limited to simplified settings like bandit tasks, which do not involve learning a new input-output mapping from scratch. In contrast, animals must often learn new behaviors de novo, which poses a rich challenge for learning-rule inference. We target this problem by inferring learning rules directly from animal decision-making data during de novo task learning, a setting that requires models flexible enough to capture suboptimality, history dependence, and rich external stimulus integration without strong structural priors. We first propose a nonparametric framework that parameterizes the per-trial update of policy weights with a deep neural network (DNN), and validate it by recovering ground-truth rules in simulation. We then extend to a recurrent variant (RNN) that captures non-Markovian dynamics by allowing updates to depend on trial history. Applied to a large behavioral dataset of mice learning a sensory decision-making task over multiple weeks, our models improved predictions on held-out data. The inferred rules revealed asymmetric updates after correct versus error trials and history dependence, consistent with non-Markovian learning. Overall, these results introduce a flexible framework for inferring biological learning rules from behavioral data in de novo learning tasks, providing insights to inform experimental training protocols and the development of behavioral digital twins.

System Identification for Continuous-time Linear Dynamical Systems

The problem of system identification for the Kalman filter, relying on the expectation-maximization (EM) procedure to learn the underlying parameters of a dynamical system, has largely been studied assuming that observations are sampled at equally-spaced time points. However, in many applications this is a restrictive and unrealistic assumption. This paper addresses system identification for the continuous-discrete filter, with the aim of generalizing learning for the Kalman filter by relying on a solution to a continuous-time It\^o stochastic differential equation (SDE) for the latent state and covariance dynamics. We introduce a novel two-filter, analytical form for the posterior with a Bayesian derivation, which yields analytical updates which do not require the forward-pass to be pre-computed. Using this analytical and efficient computation of the posterior, we provide an EM procedure which estimates the parameters of the SDE, naturally incorporating irregularly sampled measurements. Generalizing the learning of latent linear dynamical systems (LDS) to continuous-time may extend the use of the hybrid Kalman filter to data which is not regularly sampled or has intermittent missing values, and can extend the power of non-linear system identification methods such as switching LDS (SLDS), which rely on EM for the linear discrete-time Kalman filter as a sub-unit for learning locally linearized behavior of a non-linear system. We apply the method by learning the parameters of a latent, multivariate Fokker-Planck SDE representing a toggle-switch genetic circuit using biologically realistic parameters, and compare the efficacy of learning relative to the discrete-time Kalman filter as the step-size irregularity and spectral-radius of the dynamics-matrix increases.

Neural Latents Benchmark '21: Evaluating latent variable models of neural population activity

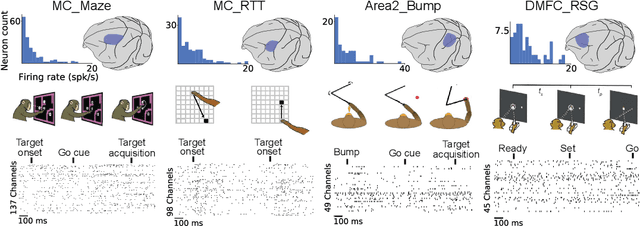
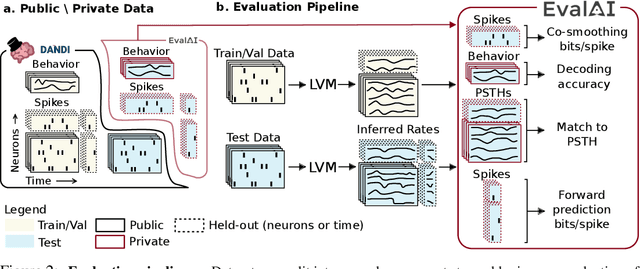
Advances in neural recording present increasing opportunities to study neural activity in unprecedented detail. Latent variable models (LVMs) are promising tools for analyzing this rich activity across diverse neural systems and behaviors, as LVMs do not depend on known relationships between the activity and external experimental variables. However, progress in latent variable modeling is currently impeded by a lack of standardization, resulting in methods being developed and compared in an ad hoc manner. To coordinate these modeling efforts, we introduce a benchmark suite for latent variable modeling of neural population activity. We curate four datasets of neural spiking activity from cognitive, sensory, and motor areas to promote models that apply to the wide variety of activity seen across these areas. We identify unsupervised evaluation as a common framework for evaluating models across datasets, and apply several baselines that demonstrate benchmark diversity. We release this benchmark through EvalAI. http://neurallatents.github.io

Fast shared response model for fMRI data

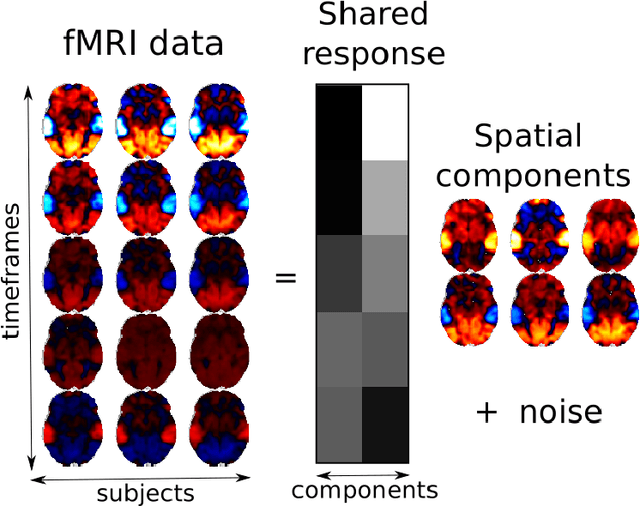
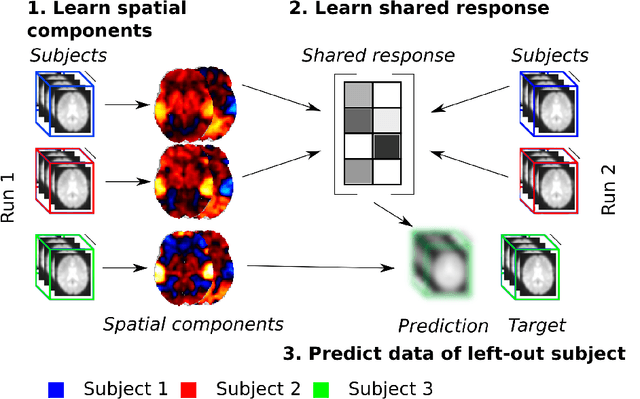
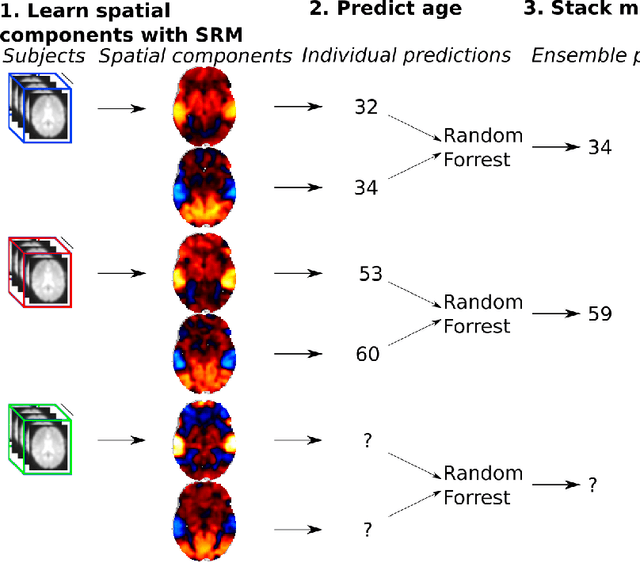
The shared response model provides a simple but effective framework toanalyse fMRI data of subjects exposed to naturalistic stimuli. However whenthe number of subjects or runs is large, fitting the model requires a large amountof memory and computational power, which limits its use in practice. In thiswork, we introduce the FastSRM algorithm that relies on an intermediate atlas-based representation. It provides considerable speed-up in time and memoryusage, hence it allows easy and fast large-scale analysis of naturalistic-stimulusfMRI data. Using four different datasets, we show that our method outperformsthe original SRM algorithm while being about 5x faster and 20x to 40x morememory efficient. Based on this contribution, we use FastSRM to predict agefrom movie watching data on the CamCAN sample. Besides delivering accuratepredictions (mean absolute error of 7.5 years), FastSRM extracts topographicpatterns that are predictive of age, demonstrating that brain activity duringfree perception reflects age.