Disentangling Interpretable Factors with Supervised Independent Subspace Principal Component Analysis

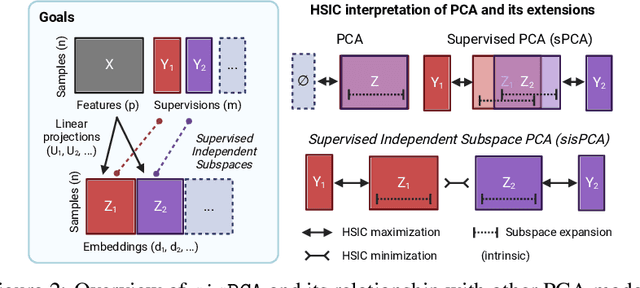
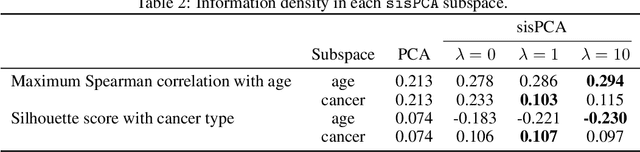
The success of machine learning models relies heavily on effectively representing high-dimensional data. However, ensuring data representations capture human-understandable concepts remains difficult, often requiring the incorporation of prior knowledge and decomposition of data into multiple subspaces. Traditional linear methods fall short in modeling more than one space, while more expressive deep learning approaches lack interpretability. Here, we introduce Supervised Independent Subspace Principal Component Analysis ($\texttt{sisPCA}$), a PCA extension designed for multi-subspace learning. Leveraging the Hilbert-Schmidt Independence Criterion (HSIC), $\texttt{sisPCA}$ incorporates supervision and simultaneously ensures subspace disentanglement. We demonstrate $\texttt{sisPCA}$'s connections with autoencoders and regularized linear regression and showcase its ability to identify and separate hidden data structures through extensive applications, including breast cancer diagnosis from image features, learning aging-associated DNA methylation changes, and single-cell analysis of malaria infection. Our results reveal distinct functional pathways associated with malaria colonization, underscoring the essentiality of explainable representation in high-dimensional data analysis.

The VampPrior Mixture Model

Current clustering priors for deep latent variable models (DLVMs) require defining the number of clusters a-priori and are susceptible to poor initializations. Addressing these deficiencies could greatly benefit deep learning-based scRNA-seq analysis by performing integration and clustering simultaneously. We adapt the VampPrior (Tomczak & Welling, 2018) into a Dirichlet process Gaussian mixture model, resulting in the VampPrior Mixture Model (VMM), a novel prior for DLVMs. We propose an inference procedure that alternates between variational inference and Empirical Bayes to cleanly distinguish variational and prior parameters. Using the VMM in a Variational Autoencoder attains highly competitive clustering performance on benchmark datasets. Augmenting scVI (Lopez et al., 2018), a popular scRNA-seq integration method, with the VMM significantly improves its performance and automatically arranges cells into biologically meaningful clusters.

System Identification for Continuous-time Linear Dynamical Systems

The problem of system identification for the Kalman filter, relying on the expectation-maximization (EM) procedure to learn the underlying parameters of a dynamical system, has largely been studied assuming that observations are sampled at equally-spaced time points. However, in many applications this is a restrictive and unrealistic assumption. This paper addresses system identification for the continuous-discrete filter, with the aim of generalizing learning for the Kalman filter by relying on a solution to a continuous-time It\^o stochastic differential equation (SDE) for the latent state and covariance dynamics. We introduce a novel two-filter, analytical form for the posterior with a Bayesian derivation, which yields analytical updates which do not require the forward-pass to be pre-computed. Using this analytical and efficient computation of the posterior, we provide an EM procedure which estimates the parameters of the SDE, naturally incorporating irregularly sampled measurements. Generalizing the learning of latent linear dynamical systems (LDS) to continuous-time may extend the use of the hybrid Kalman filter to data which is not regularly sampled or has intermittent missing values, and can extend the power of non-linear system identification methods such as switching LDS (SLDS), which rely on EM for the linear discrete-time Kalman filter as a sub-unit for learning locally linearized behavior of a non-linear system. We apply the method by learning the parameters of a latent, multivariate Fokker-Planck SDE representing a toggle-switch genetic circuit using biologically realistic parameters, and compare the efficacy of learning relative to the discrete-time Kalman filter as the step-size irregularity and spectral-radius of the dynamics-matrix increases.

Vector Embeddings by Sequence Similarity and Context for Improved Compression, Similarity Search, Clustering, Organization, and Manipulation of cDNA Libraries

This paper demonstrates the utility of organized numerical representations of genes in research involving flat string gene formats (i.e., FASTA/FASTQ5). FASTA/FASTQ files have several current limitations, such as their large file sizes, slow processing speeds for mapping and alignment, and contextual dependencies. These challenges significantly hinder investigations and tasks that involve finding similar sequences. The solution lies in transforming sequences into an alternative representation that facilitates easier clustering into similar groups compared to the raw sequences themselves. By assigning a unique vector embedding to each short sequence, it is possible to more efficiently cluster and improve upon compression performance for the string representations of cDNA libraries. Furthermore, through learning alternative coordinate vector embeddings based on the contexts of codon triplets, we can demonstrate clustering based on amino acid properties. Finally, using this sequence embedding method to encode barcodes and cDNA sequences, we can improve the time complexity of the similarity search by coupling vector embeddings with an algorithm that determines the proximity of vectors in Euclidean space; this allows us to perform sequence similarity searches in a quicker and more modular fashion.

Faithful Heteroscedastic Regression with Neural Networks

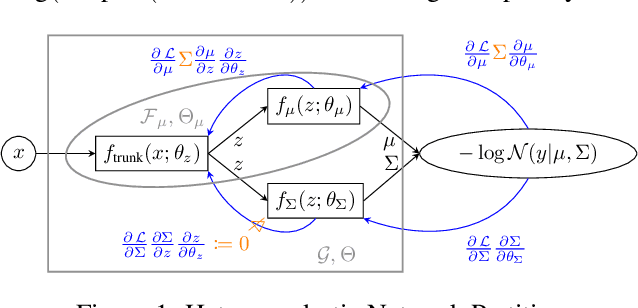
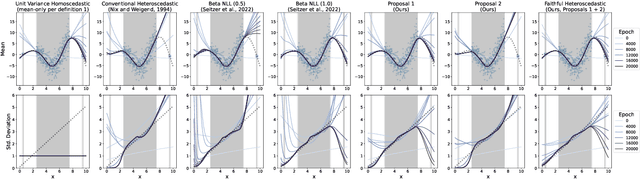
Heteroscedastic regression models a Gaussian variable's mean and variance as a function of covariates. Parametric methods that employ neural networks for these parameter maps can capture complex relationships in the data. Yet, optimizing network parameters via log likelihood gradients can yield suboptimal mean and uncalibrated variance estimates. Current solutions side-step this optimization problem with surrogate objectives or Bayesian treatments. Instead, we make two simple modifications to optimization. Notably, their combination produces a heteroscedastic model with mean estimates that are provably as accurate as those from its homoscedastic counterpart (i.e.~fitting the mean under squared error loss). For a wide variety of network and task complexities, we find that mean estimates from existing heteroscedastic solutions can be significantly less accurate than those from an equivalently expressive mean-only model. Our approach provably retains the accuracy of an equally flexible mean-only model while also offering best-in-class variance calibration. Lastly, we show how to leverage our method to recover the underlying heteroscedastic noise variance.

Variational Variance: Simple and Reliable Predictive Variance Parameterization

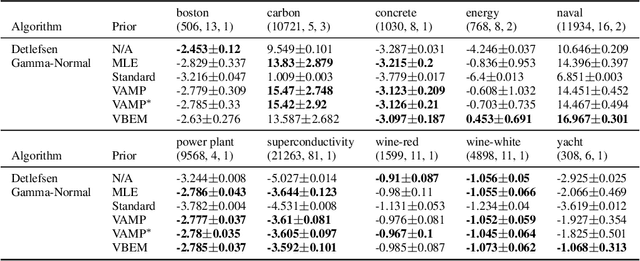
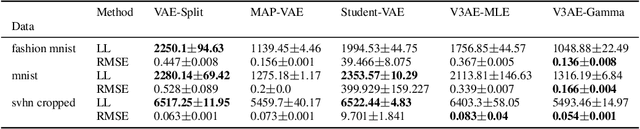
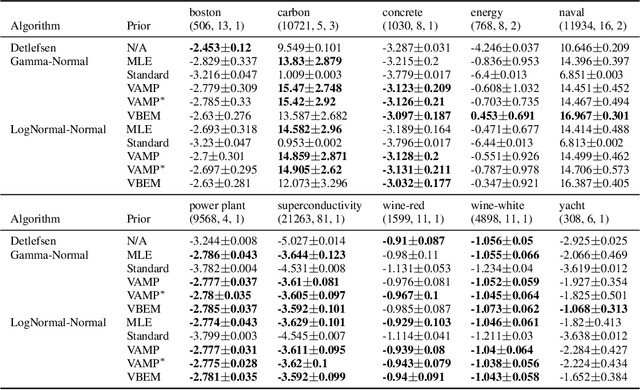
An often overlooked sleight of hand performed with variational autoencoders (VAEs), which has proliferated the literature, is to misrepresent the posterior predictive (decoder) distribution's expectation as a sample from that distribution. Jointly modeling the mean and variance for a normal predictive distribution can result in fragile optimization where the ultimately learned parameters can be ineffective at generating realistic samples. The two most common principled methods to avoid this problem are to either fix the variance or use the single-parameter Bernoulli distribution--both have drawbacks, however. Unfortunately, the problem of jointly optimizing mean and variance networks affects not only unsupervised modeling of continuous data (a taxonomy for many VAE applications) but also regression tasks. To date, only a handful of papers have attempted to resolve these difficulties. In this article, we propose an alternative and attractively simple solution: treat predictive variance variationally. Our approach synergizes with existing VAE-specific theoretical results and, being probabilistically principled, provides access to Empirical Bayes and other such techniques that utilize the observed data to construct well-informed priors. We extend the VAMP prior, which assumes a uniform mixture, by inferring mixture proportions and assignments. This extension amplifies our ability to accurately capture heteroscedastic variance. Notably, our methods experimentally outperform existing techniques on supervised and unsupervised modeling of continuous data.

Stochastic gradient variational Bayes for gamma approximating distributions

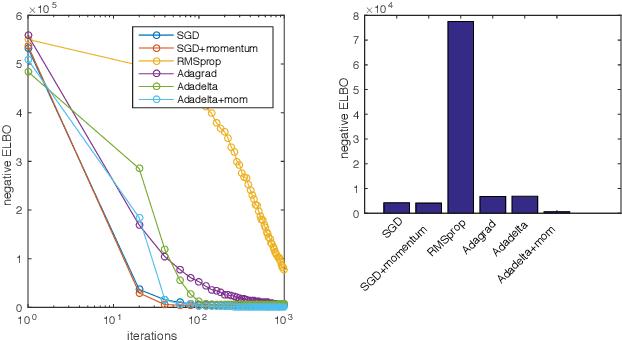
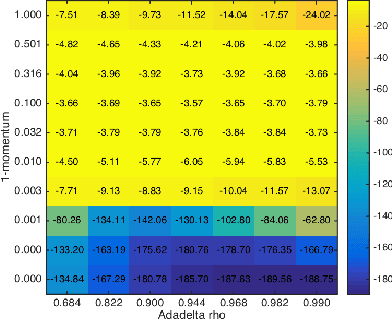
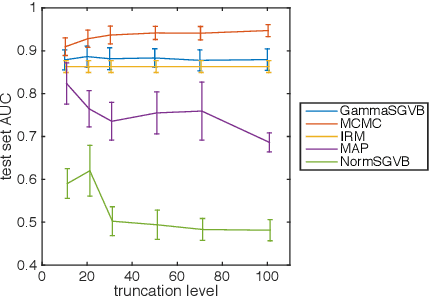
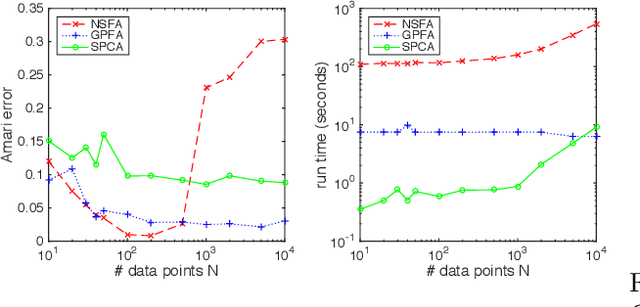
While stochastic variational inference is relatively well known for scaling inference in Bayesian probabilistic models, related methods also offer ways to circumnavigate the approximation of analytically intractable expectations. The key challenge in either setting is controlling the variance of gradient estimates: recent work has shown that for continuous latent variables, particularly multivariate Gaussians, this can be achieved by using the gradient of the log posterior. In this paper we apply the same idea to gamma distributed latent variables given gamma variational distributions, enabling straightforward "black box" variational inference in models where sparsity and non-negativity are appropriate. We demonstrate the method on a recently proposed gamma process model for network data, as well as a novel sparse factor analysis. We outperform generic sampling algorithms and the approach of using Gaussian variational distributions on transformed variables.

An Empirical Study of Stochastic Variational Algorithms for the Beta Bernoulli Process

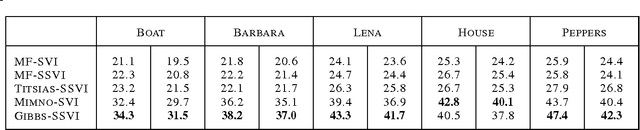
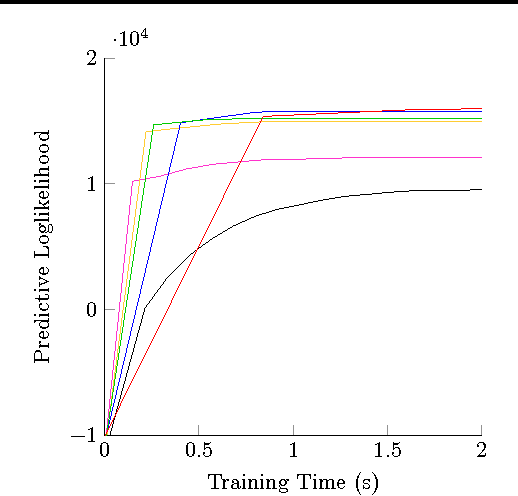
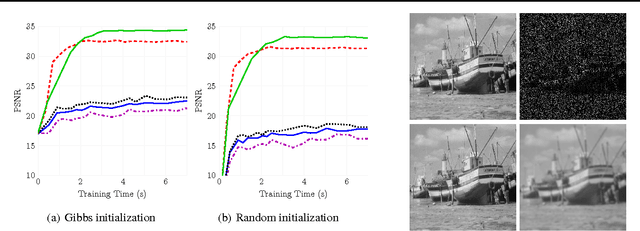
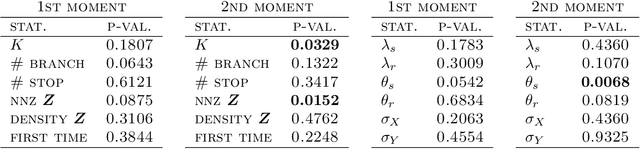
Stochastic variational inference (SVI) is emerging as the most promising candidate for scaling inference in Bayesian probabilistic models to large datasets. However, the performance of these methods has been assessed primarily in the context of Bayesian topic models, particularly latent Dirichlet allocation (LDA). Deriving several new algorithms, and using synthetic, image and genomic datasets, we investigate whether the understanding gleaned from LDA applies in the setting of sparse latent factor models, specifically beta process factor analysis (BPFA). We demonstrate that the big picture is consistent: using Gibbs sampling within SVI to maintain certain posterior dependencies is extremely effective. However, we find that different posterior dependencies are important in BPFA relative to LDA. Particularly, approximations able to model intra-local variable dependence perform best.

Beta diffusion trees and hierarchical feature allocations

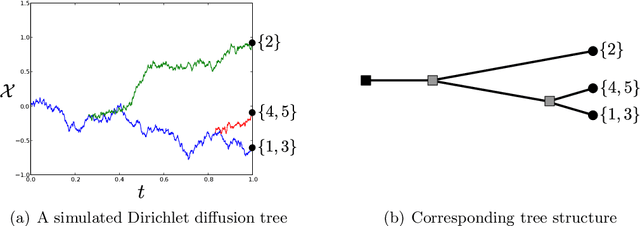
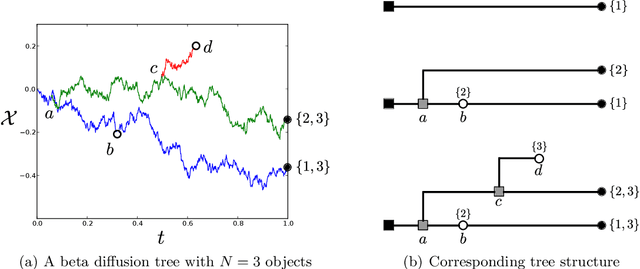
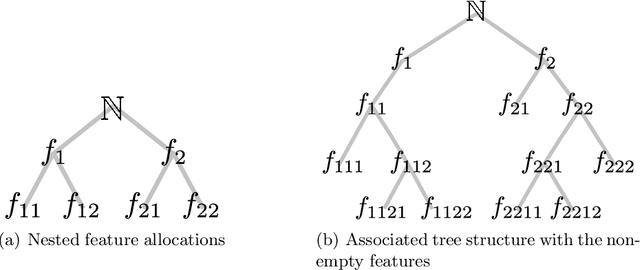
We define the beta diffusion tree, a random tree structure with a set of leaves that defines a collection of overlapping subsets of objects, known as a feature allocation. A generative process for the tree structure is defined in terms of particles (representing the objects) diffusing in some continuous space, analogously to the Dirichlet diffusion tree (Neal, 2003), which defines a tree structure over partitions (i.e., non-overlapping subsets) of the objects. Unlike in the Dirichlet diffusion tree, multiple copies of a particle may exist and diffuse along multiple branches in the beta diffusion tree, and an object may therefore belong to multiple subsets of particles. We demonstrate how to build a hierarchically-clustered factor analysis model with the beta diffusion tree and how to perform inference over the random tree structures with a Markov chain Monte Carlo algorithm. We conclude with several numerical experiments on missing data problems with data sets of gene expression microarrays, international development statistics, and intranational socioeconomic measurements.

Fixed-Form Variational Posterior Approximation through Stochastic Linear Regression

We propose a general algorithm for approximating nonstandard Bayesian posterior distributions. The algorithm minimizes the Kullback-Leibler divergence of an approximating distribution to the intractable posterior distribution. Our method can be used to approximate any posterior distribution, provided that it is given in closed form up to the proportionality constant. The approximation can be any distribution in the exponential family or any mixture of such distributions, which means that it can be made arbitrarily precise. Several examples illustrate the speed and accuracy of our approximation method in practice.