Active learning for efficient discovery of optimal gene combinations in the combinatorial perturbation space

The advancement of novel combinatorial CRISPR screening technologies enables the identification of synergistic gene combinations on a large scale. This is crucial for developing novel and effective combination therapies, but the combinatorial space makes exhaustive experimentation infeasible. We introduce NAIAD, an active learning framework that efficiently discovers optimal gene pairs capable of driving cells toward desired cellular phenotypes. NAIAD leverages single-gene perturbation effects and adaptive gene embeddings that scale with the training data size, mitigating overfitting in small-sample learning while capturing complex gene interactions as more data is collected. Evaluated on four CRISPR combinatorial perturbation datasets totaling over 350,000 genetic interactions, NAIAD, trained on small datasets, outperforms existing models by up to 40\% relative to the second-best. NAIAD's recommendation system prioritizes gene pairs with the maximum predicted effects, resulting in the highest marginal gain in each AI-experiment round and accelerating discovery with fewer CRISPR experimental iterations. Our NAIAD framework (https://github.com/NeptuneBio/NAIAD) improves the identification of novel, effective gene combinations, enabling more efficient CRISPR library design and offering promising applications in genomics research and therapeutic development.

Faithful Heteroscedastic Regression with Neural Networks

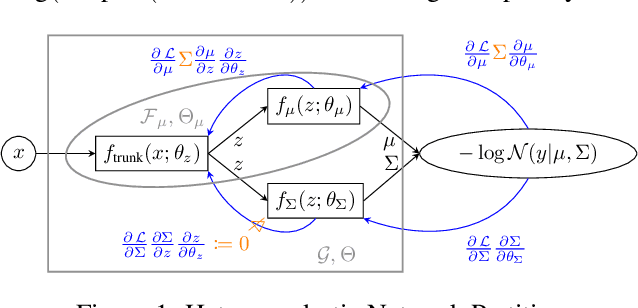
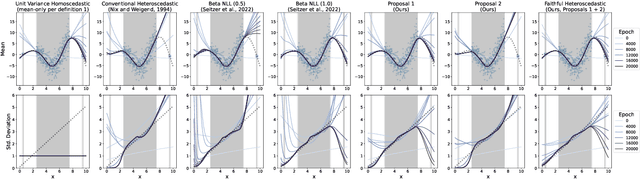
Heteroscedastic regression models a Gaussian variable's mean and variance as a function of covariates. Parametric methods that employ neural networks for these parameter maps can capture complex relationships in the data. Yet, optimizing network parameters via log likelihood gradients can yield suboptimal mean and uncalibrated variance estimates. Current solutions side-step this optimization problem with surrogate objectives or Bayesian treatments. Instead, we make two simple modifications to optimization. Notably, their combination produces a heteroscedastic model with mean estimates that are provably as accurate as those from its homoscedastic counterpart (i.e.~fitting the mean under squared error loss). For a wide variety of network and task complexities, we find that mean estimates from existing heteroscedastic solutions can be significantly less accurate than those from an equivalently expressive mean-only model. Our approach provably retains the accuracy of an equally flexible mean-only model while also offering best-in-class variance calibration. Lastly, we show how to leverage our method to recover the underlying heteroscedastic noise variance.