The VampPrior Mixture Model

Current clustering priors for deep latent variable models (DLVMs) require defining the number of clusters a-priori and are susceptible to poor initializations. Addressing these deficiencies could greatly benefit deep learning-based scRNA-seq analysis by performing integration and clustering simultaneously. We adapt the VampPrior (Tomczak & Welling, 2018) into a Dirichlet process Gaussian mixture model, resulting in the VampPrior Mixture Model (VMM), a novel prior for DLVMs. We propose an inference procedure that alternates between variational inference and Empirical Bayes to cleanly distinguish variational and prior parameters. Using the VMM in a Variational Autoencoder attains highly competitive clustering performance on benchmark datasets. Augmenting scVI (Lopez et al., 2018), a popular scRNA-seq integration method, with the VMM significantly improves its performance and automatically arranges cells into biologically meaningful clusters.

Faithful Heteroscedastic Regression with Neural Networks

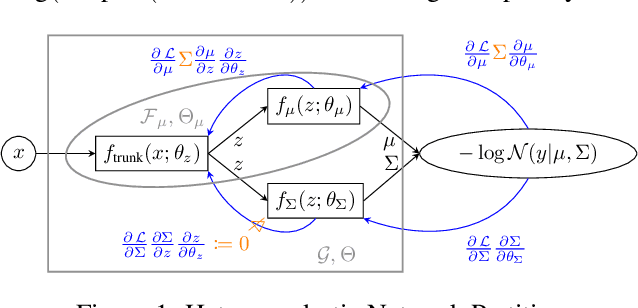
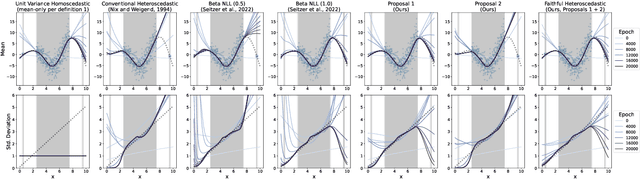
Heteroscedastic regression models a Gaussian variable's mean and variance as a function of covariates. Parametric methods that employ neural networks for these parameter maps can capture complex relationships in the data. Yet, optimizing network parameters via log likelihood gradients can yield suboptimal mean and uncalibrated variance estimates. Current solutions side-step this optimization problem with surrogate objectives or Bayesian treatments. Instead, we make two simple modifications to optimization. Notably, their combination produces a heteroscedastic model with mean estimates that are provably as accurate as those from its homoscedastic counterpart (i.e.~fitting the mean under squared error loss). For a wide variety of network and task complexities, we find that mean estimates from existing heteroscedastic solutions can be significantly less accurate than those from an equivalently expressive mean-only model. Our approach provably retains the accuracy of an equally flexible mean-only model while also offering best-in-class variance calibration. Lastly, we show how to leverage our method to recover the underlying heteroscedastic noise variance.

Variational Variance: Simple and Reliable Predictive Variance Parameterization

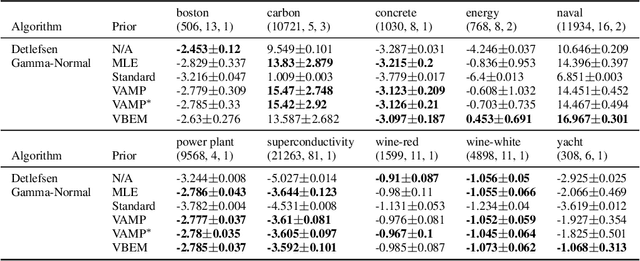
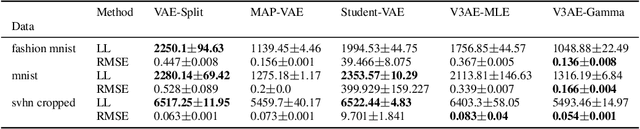
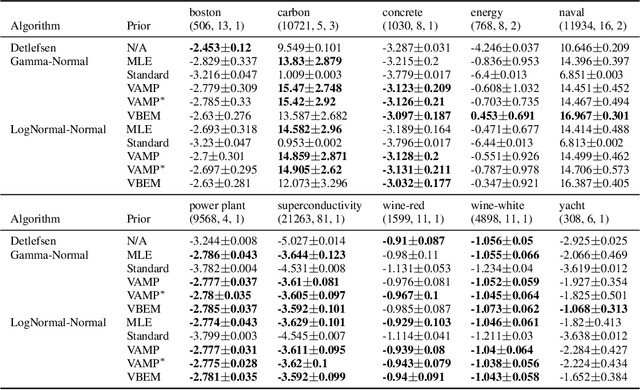
An often overlooked sleight of hand performed with variational autoencoders (VAEs), which has proliferated the literature, is to misrepresent the posterior predictive (decoder) distribution's expectation as a sample from that distribution. Jointly modeling the mean and variance for a normal predictive distribution can result in fragile optimization where the ultimately learned parameters can be ineffective at generating realistic samples. The two most common principled methods to avoid this problem are to either fix the variance or use the single-parameter Bernoulli distribution--both have drawbacks, however. Unfortunately, the problem of jointly optimizing mean and variance networks affects not only unsupervised modeling of continuous data (a taxonomy for many VAE applications) but also regression tasks. To date, only a handful of papers have attempted to resolve these difficulties. In this article, we propose an alternative and attractively simple solution: treat predictive variance variationally. Our approach synergizes with existing VAE-specific theoretical results and, being probabilistically principled, provides access to Empirical Bayes and other such techniques that utilize the observed data to construct well-informed priors. We extend the VAMP prior, which assumes a uniform mixture, by inferring mixture proportions and assignments. This extension amplifies our ability to accurately capture heteroscedastic variance. Notably, our methods experimentally outperform existing techniques on supervised and unsupervised modeling of continuous data.

A New Distribution on the Simplex with Auto-Encoding Applications

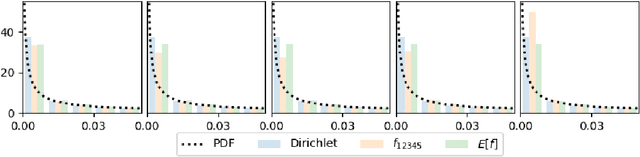
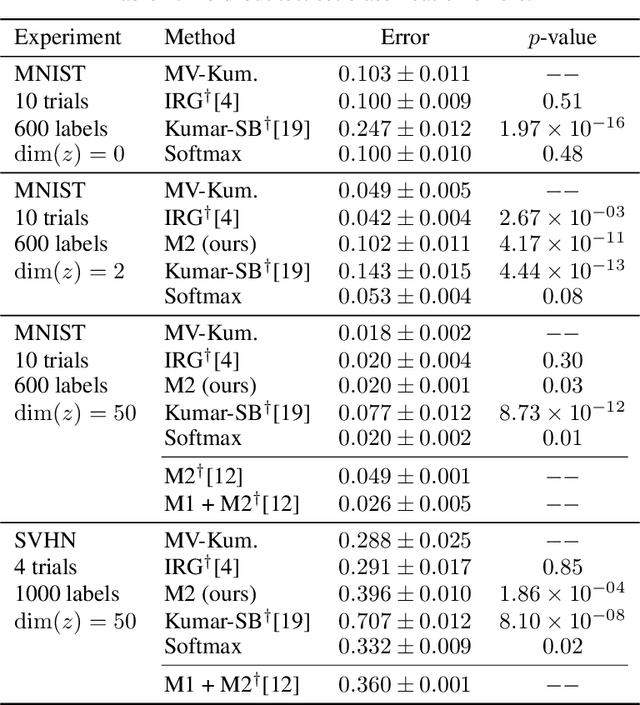
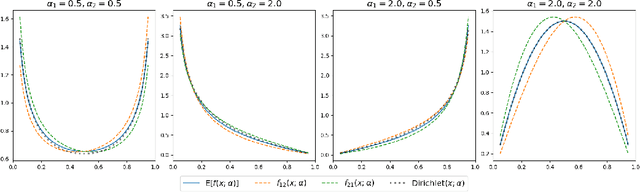
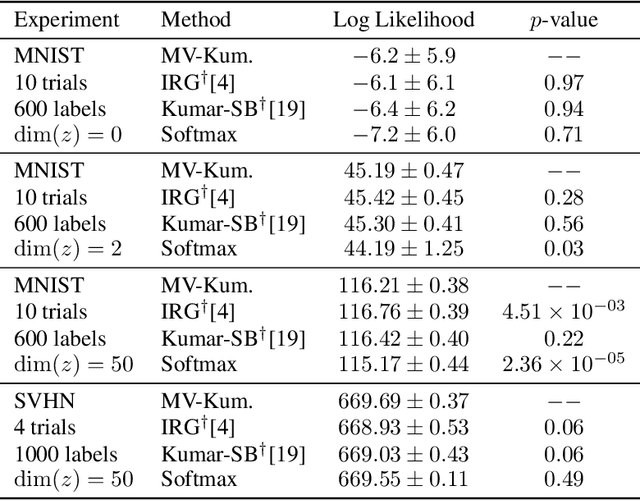
We construct a new distribution for the simplex using the Kumaraswamy distribution and an ordered stick-breaking process. We explore and develop the theoretical properties of this new distribution and prove that it exhibits symmetry under the same conditions as the well-known Dirichlet. Like the Dirichlet, the new distribution is adept at capturing sparsity but, unlike the Dirichlet, has an exact and closed form reparameterization--making it well suited for deep variational Bayesian modeling. We demonstrate the distribution's utility in a variety of semi-supervised auto-encoding tasks. In all cases, the resulting models achieve competitive performance commensurate with their simplicity, use of explicit probability models, and abstinence from adversarial training.

Thompson Sampling for Noncompliant Bandits

Thompson sampling, a Bayesian method for balancing exploration and exploitation in bandit problems, has theoretical guarantees and exhibits strong empirical performance in many domains. Traditional Thompson sampling, however, assumes perfect compliance, where an agent's chosen action is treated as the implemented action. This article introduces a stochastic noncompliance model that relaxes this assumption. We prove that any noncompliance in a 2-armed Bernoulli bandit increases existing regret bounds. With our noncompliance model, we derive Thompson sampling variants that explicitly handle both observed and latent noncompliance. With extensive empirical analysis, we demonstrate that our algorithms either match or outperform traditional Thompson sampling in both compliant and noncompliant environments.