Variational Variance: Simple and Reliable Predictive Variance Parameterization
Paper and Code
Jun 11, 2020
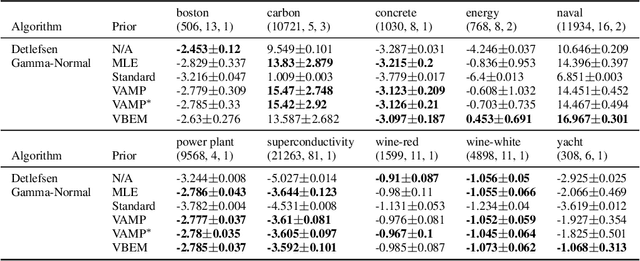
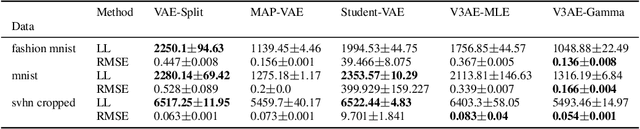
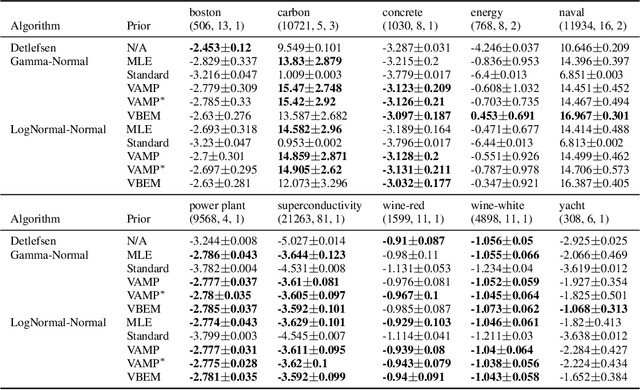
An often overlooked sleight of hand performed with variational autoencoders (VAEs), which has proliferated the literature, is to misrepresent the posterior predictive (decoder) distribution's expectation as a sample from that distribution. Jointly modeling the mean and variance for a normal predictive distribution can result in fragile optimization where the ultimately learned parameters can be ineffective at generating realistic samples. The two most common principled methods to avoid this problem are to either fix the variance or use the single-parameter Bernoulli distribution--both have drawbacks, however. Unfortunately, the problem of jointly optimizing mean and variance networks affects not only unsupervised modeling of continuous data (a taxonomy for many VAE applications) but also regression tasks. To date, only a handful of papers have attempted to resolve these difficulties. In this article, we propose an alternative and attractively simple solution: treat predictive variance variationally. Our approach synergizes with existing VAE-specific theoretical results and, being probabilistically principled, provides access to Empirical Bayes and other such techniques that utilize the observed data to construct well-informed priors. We extend the VAMP prior, which assumes a uniform mixture, by inferring mixture proportions and assignments. This extension amplifies our ability to accurately capture heteroscedastic variance. Notably, our methods experimentally outperform existing techniques on supervised and unsupervised modeling of continuous data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge