A New Distribution on the Simplex with Auto-Encoding Applications
Paper and Code
May 28, 2019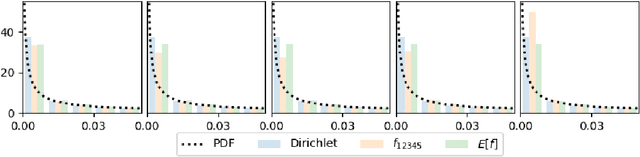
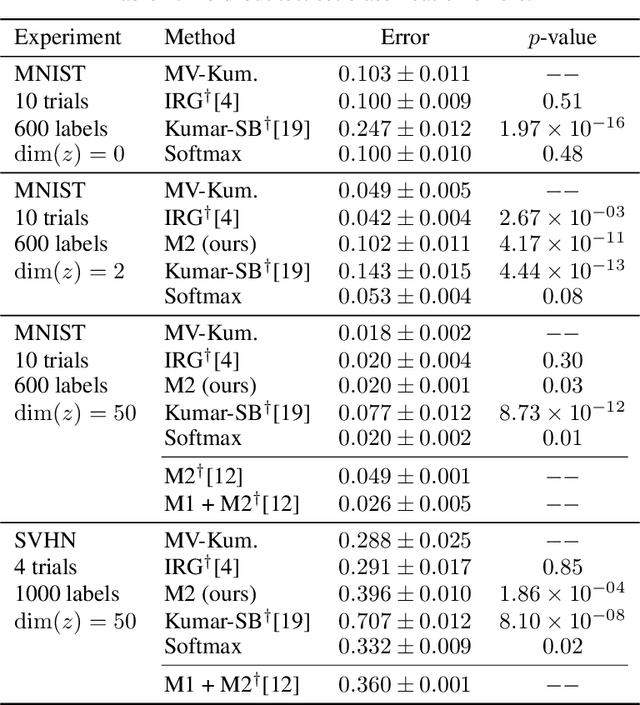
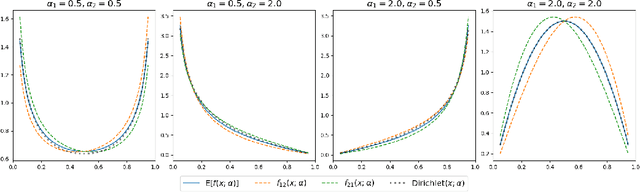
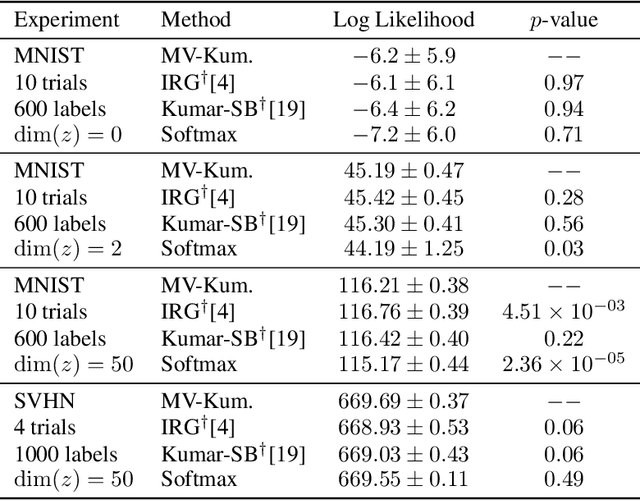
We construct a new distribution for the simplex using the Kumaraswamy distribution and an ordered stick-breaking process. We explore and develop the theoretical properties of this new distribution and prove that it exhibits symmetry under the same conditions as the well-known Dirichlet. Like the Dirichlet, the new distribution is adept at capturing sparsity but, unlike the Dirichlet, has an exact and closed form reparameterization--making it well suited for deep variational Bayesian modeling. We demonstrate the distribution's utility in a variety of semi-supervised auto-encoding tasks. In all cases, the resulting models achieve competitive performance commensurate with their simplicity, use of explicit probability models, and abstinence from adversarial training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge