Active Learning in CNNs via Expected Improvement Maximization

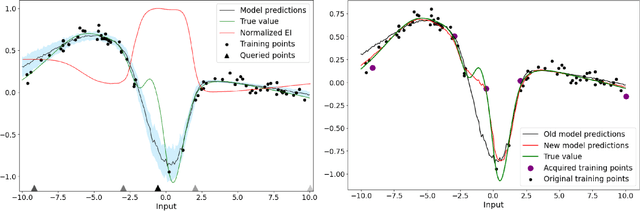
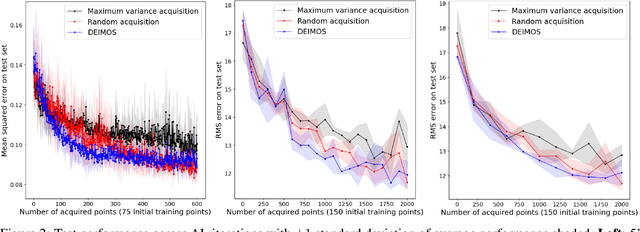
Deep learning models such as Convolutional Neural Networks (CNNs) have demonstrated high levels of effectiveness in a variety of domains, including computer vision and more recently, computational biology. However, training effective models often requires assembling and/or labeling large datasets, which may be prohibitively time-consuming or costly. Pool-based active learning techniques have the potential to mitigate these issues, leveraging models trained on limited data to selectively query unlabeled data points from a pool in an attempt to expedite the learning process. Here we present "Dropout-based Expected IMprOvementS" (DEIMOS), a flexible and computationally-efficient approach to active learning that queries points that are expected to maximize the model's improvement across a representative sample of points. The proposed framework enables us to maintain a prediction covariance matrix capturing model uncertainty, and to dynamically update this matrix in order to generate diverse batches of points in the batch-mode setting. Our active learning results demonstrate that DEIMOS outperforms several existing baselines across multiple regression and classification tasks taken from computer vision and genomics.

A New Distribution on the Simplex with Auto-Encoding Applications

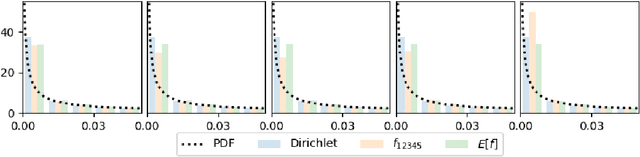
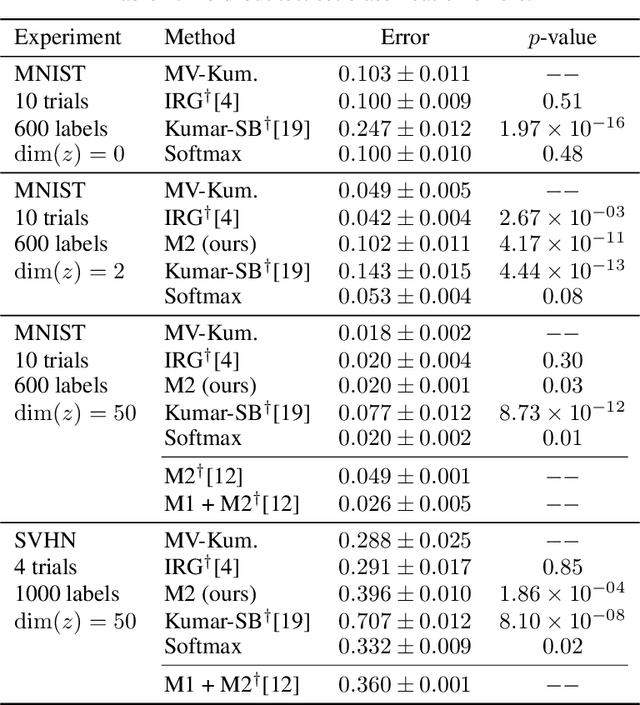
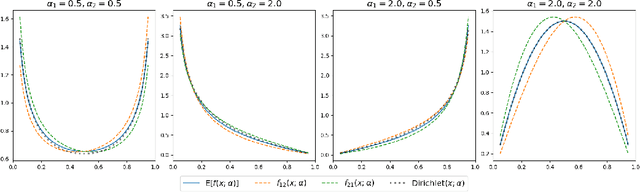
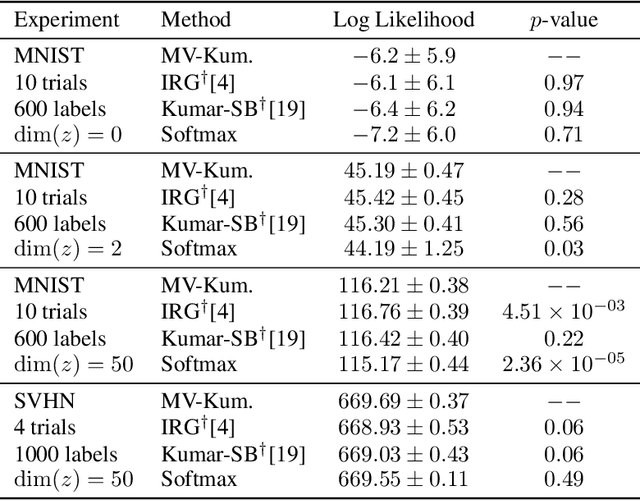
We construct a new distribution for the simplex using the Kumaraswamy distribution and an ordered stick-breaking process. We explore and develop the theoretical properties of this new distribution and prove that it exhibits symmetry under the same conditions as the well-known Dirichlet. Like the Dirichlet, the new distribution is adept at capturing sparsity but, unlike the Dirichlet, has an exact and closed form reparameterization--making it well suited for deep variational Bayesian modeling. We demonstrate the distribution's utility in a variety of semi-supervised auto-encoding tasks. In all cases, the resulting models achieve competitive performance commensurate with their simplicity, use of explicit probability models, and abstinence from adversarial training.