An Eager Satisfiability Modulo Theories Solver for Algebraic Datatypes

Algebraic data types (ADTs) are a construct classically found in functional programming languages that capture data structures like enumerated types, lists, and trees. In recent years, interest in ADTs has increased. For example, popular programming languages, like Python, have added support for ADTs. Automated reasoning about ADTs can be done using satisfiability modulo theories (SMT) solving, an extension of the Boolean satisfiability problem with constraints over first-order structures. Unfortunately, SMT solvers that support ADTs do not scale as state-of-the-art approaches all use variations of the same \emph{lazy} approach. In this paper, we present an SMT solver that takes a fundamentally different approach, an \emph{eager} approach. Specifically, our solver reduces ADT queries to a simpler logical theory, uninterpreted functions (UF), and then uses an existing solver on the reduced query. We prove the soundness and completeness of our approach and demonstrate that it outperforms the state-of-theart on existing benchmarks, as well as a new, more challenging benchmark set from the planning domain.

Recovery of Meteorites Using an Autonomous Drone and Machine Learning

The recovery of freshly fallen meteorites from tracked and triangulated meteors is critical to determining their source asteroid families. However, locating meteorite fragments in strewn fields remains a challenge with very few meteorites being recovered from the meteors triangulated in past and ongoing meteor camera networks. We examined if locating meteorites can be automated using machine learning and an autonomous drone. Drones can be programmed to fly a grid search pattern and take systematic pictures of the ground over a large survey area. Those images can be analyzed using a machine learning classifier to identify meteorites in the field among many other features. Here, we describe a proof-of-concept meteorite classifier that deploys off-line a combination of different convolution neural networks to recognize meteorites from images taken by drones in the field. The system was implemented in a conceptual drone setup and tested in the suspected strewn field of a recent meteorite fall near Walker Lake, Nevada.

Urban Driving with Conditional Imitation Learning

Hand-crafting generalised decision-making rules for real-world urban autonomous driving is hard. Alternatively, learning behaviour from easy-to-collect human driving demonstrations is appealing. Prior work has studied imitation learning (IL) for autonomous driving with a number of limitations. Examples include only performing lane-following rather than following a user-defined route, only using a single camera view or heavily cropped frames lacking state observability, only lateral (steering) control, but not longitudinal (speed) control and a lack of interaction with traffic. Importantly, the majority of such systems have been primarily evaluated in simulation - a simple domain, which lacks real-world complexities. Motivated by these challenges, we focus on learning representations of semantics, geometry and motion with computer vision for IL from human driving demonstrations. As our main contribution, we present an end-to-end conditional imitation learning approach, combining both lateral and longitudinal control on a real vehicle for following urban routes with simple traffic. We address inherent dataset bias by data balancing, training our final policy on approximately 30 hours of demonstrations gathered over six months. We evaluate our method on an autonomous vehicle by driving 35km of novel routes in European urban streets.

Learning to Drive in a Day

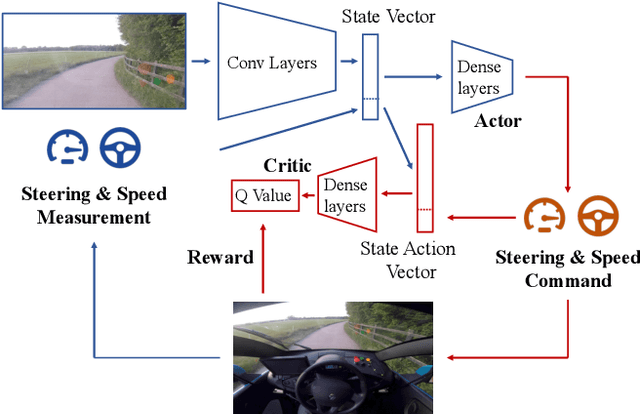
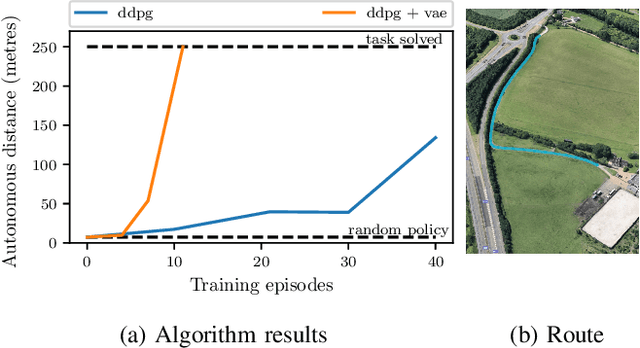
We demonstrate the first application of deep reinforcement learning to autonomous driving. From randomly initialised parameters, our model is able to learn a policy for lane following in a handful of training episodes using a single monocular image as input. We provide a general and easy to obtain reward: the distance travelled by the vehicle without the safety driver taking control. We use a continuous, model-free deep reinforcement learning algorithm, with all exploration and optimisation performed on-vehicle. This demonstrates a new framework for autonomous driving which moves away from reliance on defined logical rules, mapping, and direct supervision. We discuss the challenges and opportunities to scale this approach to a broader range of autonomous driving tasks.

Unitary Evolution Recurrent Neural Networks

Recurrent neural networks (RNNs) are notoriously difficult to train. When the eigenvalues of the hidden to hidden weight matrix deviate from absolute value 1, optimization becomes difficult due to the well studied issue of vanishing and exploding gradients, especially when trying to learn long-term dependencies. To circumvent this problem, we propose a new architecture that learns a unitary weight matrix, with eigenvalues of absolute value exactly 1. The challenge we address is that of parametrizing unitary matrices in a way that does not require expensive computations (such as eigendecomposition) after each weight update. We construct an expressive unitary weight matrix by composing several structured matrices that act as building blocks with parameters to be learned. Optimization with this parameterization becomes feasible only when considering hidden states in the complex domain. We demonstrate the potential of this architecture by achieving state of the art results in several hard tasks involving very long-term dependencies.

Predictive Entropy Search for Multi-objective Bayesian Optimization

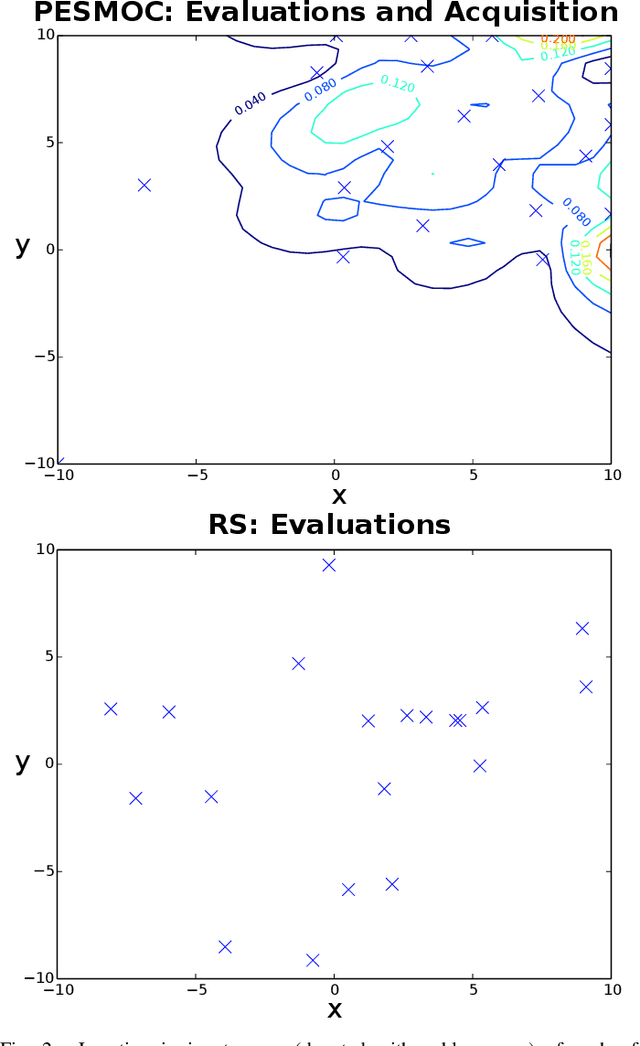
We present PESMO, a Bayesian method for identifying the Pareto set of multi-objective optimization problems, when the functions are expensive to evaluate. The central idea of PESMO is to choose evaluation points so as to maximally reduce the entropy of the posterior distribution over the Pareto set. Critically, the PESMO multi-objective acquisition function can be decomposed as a sum of objective-specific acquisition functions, which enables the algorithm to be used in \emph{decoupled} scenarios in which the objectives can be evaluated separately and perhaps with different costs. This decoupling capability also makes it possible to identify difficult objectives that require more evaluations. PESMO also offers gains in efficiency, as its cost scales linearly with the number of objectives, in comparison to the exponential cost of other methods. We compare PESMO with other related methods for multi-objective Bayesian optimization on synthetic and real-world problems. The results show that PESMO produces better recommendations with a smaller number of evaluations of the objectives, and that a decoupled evaluation can lead to improvements in performance, particularly when the number of objectives is large.

Parallel Predictive Entropy Search for Batch Global Optimization of Expensive Objective Functions

We develop parallel predictive entropy search (PPES), a novel algorithm for Bayesian optimization of expensive black-box objective functions. At each iteration, PPES aims to select a batch of points which will maximize the information gain about the global maximizer of the objective. Well known strategies exist for suggesting a single evaluation point based on previous observations, while far fewer are known for selecting batches of points to evaluate in parallel. The few batch selection schemes that have been studied all resort to greedy methods to compute an optimal batch. To the best of our knowledge, PPES is the first non-greedy batch Bayesian optimization strategy. We demonstrate the benefit of this approach in optimization performance on both synthetic and real world applications, including problems in machine learning, rocket science and robotics.

An Empirical Study of Stochastic Variational Algorithms for the Beta Bernoulli Process

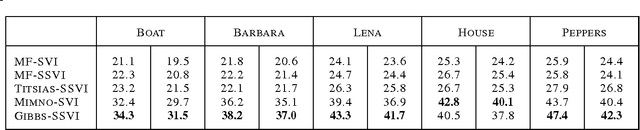
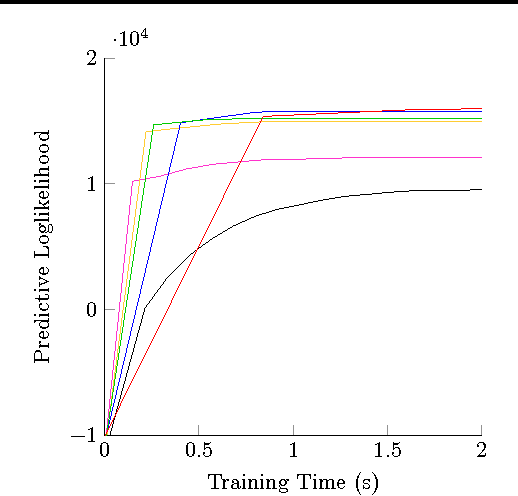
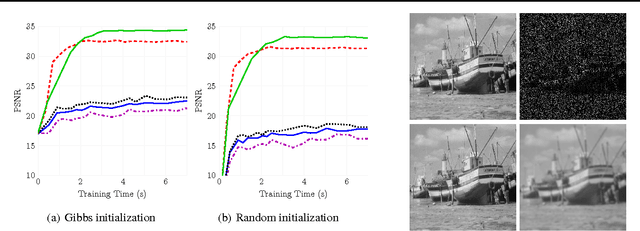
Stochastic variational inference (SVI) is emerging as the most promising candidate for scaling inference in Bayesian probabilistic models to large datasets. However, the performance of these methods has been assessed primarily in the context of Bayesian topic models, particularly latent Dirichlet allocation (LDA). Deriving several new algorithms, and using synthetic, image and genomic datasets, we investigate whether the understanding gleaned from LDA applies in the setting of sparse latent factor models, specifically beta process factor analysis (BPFA). We demonstrate that the big picture is consistent: using Gibbs sampling within SVI to maintain certain posterior dependencies is extremely effective. However, we find that different posterior dependencies are important in BPFA relative to LDA. Particularly, approximations able to model intra-local variable dependence perform best.

Student-t Processes as Alternatives to Gaussian Processes

We investigate the Student-t process as an alternative to the Gaussian process as a nonparametric prior over functions. We derive closed form expressions for the marginal likelihood and predictive distribution of a Student-t process, by integrating away an inverse Wishart process prior over the covariance kernel of a Gaussian process model. We show surprising equivalences between different hierarchical Gaussian process models leading to Student-t processes, and derive a new sampling scheme for the inverse Wishart process, which helps elucidate these equivalences. Overall, we show that a Student-t process can retain the attractive properties of a Gaussian process -- a nonparametric representation, analytic marginal and predictive distributions, and easy model selection through covariance kernels -- but has enhanced flexibility, and predictive covariances that, unlike a Gaussian process, explicitly depend on the values of training observations. We verify empirically that a Student-t process is especially useful in situations where there are changes in covariance structure, or in applications like Bayesian optimization, where accurate predictive covariances are critical for good performance. These advantages come at no additional computational cost over Gaussian processes.

Determinantal Clustering Processes - A Nonparametric Bayesian Approach to Kernel Based Semi-Supervised Clustering

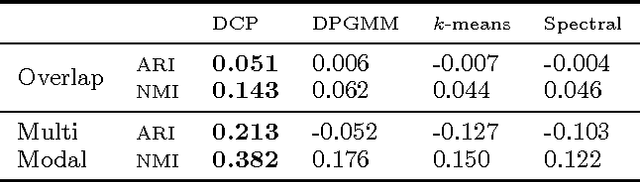
Semi-supervised clustering is the task of clustering data points into clusters where only a fraction of the points are labelled. The true number of clusters in the data is often unknown and most models require this parameter as an input. Dirichlet process mixture models are appealing as they can infer the number of clusters from the data. However, these models do not deal with high dimensional data well and can encounter difficulties in inference. We present a novel nonparameteric Bayesian kernel based method to cluster data points without the need to prespecify the number of clusters or to model complicated densities from which data points are assumed to be generated from. The key insight is to use determinants of submatrices of a kernel matrix as a measure of how close together a set of points are. We explore some theoretical properties of the model and derive a natural Gibbs based algorithm with MCMC hyperparameter learning. The model is implemented on a variety of synthetic and real world data sets.