Online Prompt and Solver Selection for Program Synthesis

Large Language Models (LLMs) demonstrate impressive capabilities in the domain of program synthesis. This level of performance is not, however, universal across all tasks, all LLMs and all prompting styles. There are many areas where one LLM dominates, one prompting style dominates, or where calling a symbolic solver is a better choice than an LLM. A key challenge for the user then, is to identify not only when an LLM is the right choice of solver, and the appropriate LLM to call for a given synthesis task, but also the right way to call it. A non-expert user who makes the wrong choice, incurs a cost both in terms of results (number of tasks solved, and the time it takes to solve them) and financial cost, if using a closed-source language model via a commercial API. We frame this choice as an online learning problem. We use a multi-armed bandit algorithm to select which symbolic solver, or LLM and prompt combination to deploy in order to maximize a given reward function (which may prioritize solving time, number of synthesis tasks solved, or financial cost of solving). We implement an instance of this approach, called CYANEA, and evaluate it on synthesis queries from the literature in ranking function synthesis, from the syntax-guided synthesis competition, and fresh, unseen queries generated from SMT problems. CYANEA solves 37.2\% more queries than the best single solver and achieves results within 4\% of the virtual best solver.

Synthetic Programming Elicitation and Repair for Text-to-Code in Very Low-Resource Programming Languages

Recent advances in large language models (LLMs) for code applications have demonstrated remarkable zero-shot fluency and instruction following on challenging code related tasks ranging from test case generation to self-repair. Unsurprisingly, however, models struggle to compose syntactically valid programs in programming languages unrepresented in pre-training, referred to as very low-resource Programming Languages (VLPLs). VLPLs appear in crucial settings including domain-specific languages for internal to tools and tool-chains and legacy languages. Inspired by an HCI technique called natural program elicitation, we propose designing an intermediate language that LLMs ``naturally'' know how to use and which can be automatically compiled to the target VLPL. Specifically, we introduce synthetic programming elicitation and compilation (SPEAK), an approach that enables LLMs to generate syntactically valid code even for VLPLs. We empirically evaluate the performance of SPEAK in a case study and find that, compared to existing retrieval and fine-tuning baselines, SPEAK produces syntactically correct programs more frequently without sacrificing semantic correctness.

An Eager Satisfiability Modulo Theories Solver for Algebraic Datatypes

Algebraic data types (ADTs) are a construct classically found in functional programming languages that capture data structures like enumerated types, lists, and trees. In recent years, interest in ADTs has increased. For example, popular programming languages, like Python, have added support for ADTs. Automated reasoning about ADTs can be done using satisfiability modulo theories (SMT) solving, an extension of the Boolean satisfiability problem with constraints over first-order structures. Unfortunately, SMT solvers that support ADTs do not scale as state-of-the-art approaches all use variations of the same \emph{lazy} approach. In this paper, we present an SMT solver that takes a fundamentally different approach, an \emph{eager} approach. Specifically, our solver reduces ADT queries to a simpler logical theory, uninterpreted functions (UF), and then uses an existing solver on the reduced query. We prove the soundness and completeness of our approach and demonstrate that it outperforms the state-of-theart on existing benchmarks, as well as a new, more challenging benchmark set from the planning domain.

String Theories involving Regular Membership Predicates: From Practice to Theory and Back

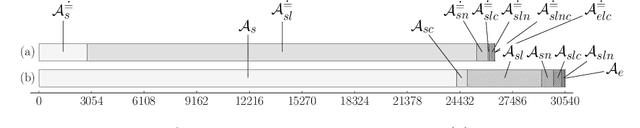
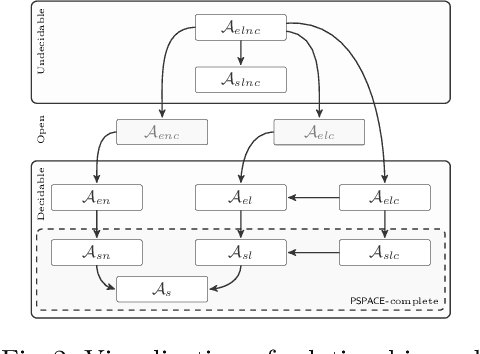
Widespread use of string solvers in formal analysis of string-heavy programs has led to a growing demand for more efficient and reliable techniques which can be applied in this context, especially for real-world cases. Designing an algorithm for the (generally undecidable) satisfiability problem for systems of string constraints requires a thorough understanding of the structure of constraints present in the targeted cases. In this paper, we investigate benchmarks presented in the literature containing regular expression membership predicates, extract different first order logic theories, and prove their decidability, resp. undecidability. Notably, the most common theories in real-world benchmarks are PSPACE-complete and directly lead to the implementation of a more efficient algorithm to solving string constraints.