$α$-$β$-Factorization and the Binary Case of Simon's Congruence

In 1991 H\'ebrard introduced a factorization of words that turned out to be a powerful tool for the investigation of a word's scattered factors (also known as (scattered) subwords or subsequences). Based on this, first Karandikar and Schnoebelen introduced the notion of $k$-richness and later on Barker et al. the notion of $k$-universality. In 2022 Fleischmann et al. presented a generalization of the arch factorization by intersecting the arch factorization of a word and its reverse. While the authors merely used this factorization for the investigation of shortest absent scattered factors, in this work we investigate this new $\alpha$-$\beta$-factorization as such. We characterize the famous Simon congruence of $k$-universal words in terms of $1$-universal words. Moreover, we apply these results to binary words. In this special case, we obtain a full characterization of the classes and calculate the index of the congruence. Lastly, we start investigating the ternary case, present a full list of possibilities for $\alpha\beta\alpha$-factors, and characterize their congruence.

On the Self Shuffle Language

The shuffle product \(u\shuffle v\) of two words \(u\) and \(v\) is the set of all words which can be obtained by interleaving \(u\) and \(v\). Motivated by the paper \emph{The Shuffle Product: New Research Directions} by Restivo (2015) we investigate a special case of the shuffle product. In this work we consider the shuffle of a word with itself called the \emph{self shuffle} or \emph{shuffle square}, showing first that the self shuffle language and the shuffle of the language are in general different sets. We prove that the language of all words arising as a self shuffle of some word is context sensitive but not context free. Furthermore, we show that the self shuffle \(w \shuffle w\) uniquely determines \(w\).

m-Nearly k-Universal Words -- Investigating Simon Congruence

Determining the index of the Simon congruence is a long outstanding open problem. Two words $u$ and $v$ are called Simon congruent if they have the same set of scattered factors, which are parts of the word in the correct order but not necessarily consecutive, e.g., $\mathtt{oath}$ is a scattered factor of $\mathtt{logarithm}$. Following the idea of scattered factor $k$-universality, we investigate $m$-nearly $k$-universality, i.e., words where $m$ scattered factors of length $k$ are absent, w.r.t. Simon congruence. We present a full characterisation as well as the index of the congruence for $m=1$. For $m\neq 1$, we show some results if in addition $w$ is $(k-1)$-universal as well as some further insights for different $m$.

Responsible and Regulatory Conform Machine Learning for Medicine: A Survey of Technical Challenges and Solutions

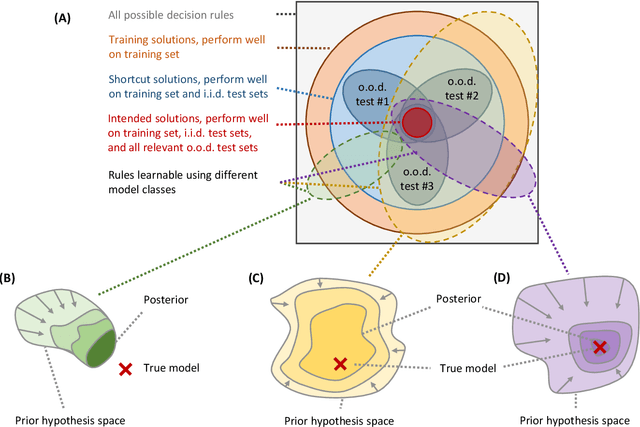
Machine learning is expected to fuel significant improvements in medical care. To ensure that fundamental principles such as beneficence, respect for human autonomy, prevention of harm, justice, privacy, and transparency are respected, medical machine learning applications must be developed responsibly. In this paper, we survey the technical challenges involved in creating medical machine learning systems responsibly and in conformity with existing regulations, as well as possible solutions to address these challenges. We begin by providing a brief overview of existing regulations affecting medical machine learning, showing that properties such as safety, robustness, reliability, privacy, security, transparency, explainability, and nondiscrimination are all demanded already by existing law and regulations - albeit, in many cases, to an uncertain degree. Next, we discuss the underlying technical challenges, possible ways for addressing them, and their respective merits and drawbacks. We notice that distribution shift, spurious correlations, model underspecification, and data scarcity represent severe challenges in the medical context (and others) that are very difficult to solve with classical black-box deep neural networks. Important measures that may help to address these challenges include the use of large and representative datasets and federated learning as a means to that end, the careful exploitation of domain knowledge wherever feasible, the use of inherently transparent models, comprehensive model testing and verification, as well as stakeholder inclusion.

String Theories involving Regular Membership Predicates: From Practice to Theory and Back

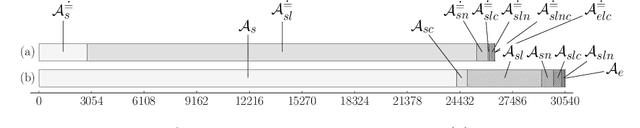
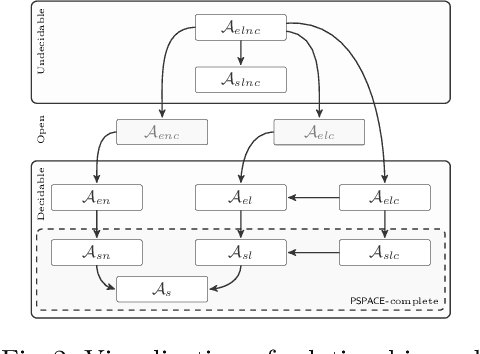
Widespread use of string solvers in formal analysis of string-heavy programs has led to a growing demand for more efficient and reliable techniques which can be applied in this context, especially for real-world cases. Designing an algorithm for the (generally undecidable) satisfiability problem for systems of string constraints requires a thorough understanding of the structure of constraints present in the targeted cases. In this paper, we investigate benchmarks presented in the literature containing regular expression membership predicates, extract different first order logic theories, and prove their decidability, resp. undecidability. Notably, the most common theories in real-world benchmarks are PSPACE-complete and directly lead to the implementation of a more efficient algorithm to solving string constraints.

Scattered Factor Universality -- The Power of the Remainder

Scattered factor (circular) universality was firstly introduced by Barker et al. in 2020. A word $w$ is called $k$-universal for some natural number $k$, if every word of length $k$ of $w$'s alphabet occurs as a scattered factor in $w$; it is called circular $k$-universal if a conjugate of $w$ is $k$-universal. Here, a word $u=u_1\cdots u_n$ is called a scattered factor of $w$ if $u$ is obtained from $w$ by deleting parts of $w$, i.e. there exists (possibly empty) words $v_1,\dots,v_{n+1}$ with $w=v_1u_1v_2\cdots v_nu_nv_{n+1}$. In this work, we prove two problems, left open in the aforementioned paper, namely a generalisation of one of their main theorems to arbitrary alphabets and a slight modification of another theorem such that we characterise the circular universality by the universality. On the way, we present deep insights into the behaviour of the remainder of the so called arch factorisation by Hebrard when repetitions of words are considered.

An Empirical Investigation of Randomized Defenses against Adversarial Attacks

In recent years, Deep Neural Networks (DNNs) have had a dramatic impact on a variety of problems that were long considered very difficult, e. g., image classification and automatic language translation to name just a few. The accuracy of modern DNNs in classification tasks is remarkable indeed. At the same time, attackers have devised powerful methods to construct specially-crafted malicious inputs (often referred to as adversarial examples) that can trick DNNs into mis-classifying them. What is worse is that despite the many defense mechanisms proposed to protect DNNs against adversarial attacks, attackers are often able to circumvent these defenses, rendering them useless. This state of affairs is extremely worrying, especially since machine learning systems get adopted at scale. In this paper, we propose a scientific evaluation methodology aimed at assessing the quality, efficacy, robustness and efficiency of randomized defenses to protect DNNs against adversarial examples. Using this methodology, we evaluate a variety of defense mechanisms. In addition, we also propose a defense mechanism we call Randomly Perturbed Ensemble Neural Networks (RPENNs). We provide a thorough and comprehensive evaluation of the considered defense mechanisms against a white-box attacker model, six different adversarial attack methods and using the ILSVRC2012 validation data set.