Report for NSF Workshop on AI for Electronic Design Automation

This report distills the discussions and recommendations from the NSF Workshop on AI for Electronic Design Automation (EDA), held on December 10, 2024 in Vancouver alongside NeurIPS 2024. Bringing together experts across machine learning and EDA, the workshop examined how AI-spanning large language models (LLMs), graph neural networks (GNNs), reinforcement learning (RL), neurosymbolic methods, etc.-can facilitate EDA and shorten design turnaround. The workshop includes four themes: (1) AI for physical synthesis and design for manufacturing (DFM), discussing challenges in physical manufacturing process and potential AI applications; (2) AI for high-level and logic-level synthesis (HLS/LLS), covering pragma insertion, program transformation, RTL code generation, etc.; (3) AI toolbox for optimization and design, discussing frontier AI developments that could potentially be applied to EDA tasks; and (4) AI for test and verification, including LLM-assisted verification tools, ML-augmented SAT solving, security/reliability challenges, etc. The report recommends NSF to foster AI/EDA collaboration, invest in foundational AI for EDA, develop robust data infrastructures, promote scalable compute infrastructure, and invest in workforce development to democratize hardware design and enable next-generation hardware systems. The workshop information can be found on the website https://ai4eda-workshop.github.io/.

FrontierCS: Evolving Challenges for Evolving Intelligence

We introduce FrontierCS, a benchmark of 156 open-ended problems across diverse areas of computer science, designed and reviewed by experts, including CS PhDs and top-tier competitive programming participants and problem setters. Unlike existing benchmarks that focus on tasks with known optimal solutions, FrontierCS targets problems where the optimal solution is unknown, but the quality of a solution can be objectively evaluated. Models solve these tasks by implementing executable programs rather than outputting a direct answer. FrontierCS includes algorithmic problems, which are often NP-hard variants of competitive programming problems with objective partial scoring, and research problems with the same property. For each problem we provide an expert reference solution and an automatic evaluator. Combining open-ended design, measurable progress, and expert curation, FrontierCS provides a benchmark at the frontier of computer-science difficulty. Empirically, we find that frontier reasoning models still lag far behind human experts on both the algorithmic and research tracks, that increasing reasoning budgets alone does not close this gap, and that models often over-optimize for generating merely workable code instead of discovering high-quality algorithms and system designs.

O-Forge: An LLM + Computer Algebra Framework for Asymptotic Analysis

Large language models have recently demonstrated advanced capabilities in solving IMO and Putnam problems; yet their role in research mathematics has remained fairly limited. The key difficulty is verification: suggested proofs may look plausible, but cannot be trusted without rigorous checking. We present a framework, called LLM+CAS, and an associated tool, O-Forge, that couples frontier LLMs with a computer algebra systems (CAS) in an In-Context Symbolic Feedback loop to produce proofs that are both creative and symbolically verified. Our focus is on asymptotic inequalities, a topic that often involves difficult proofs and appropriate decomposition of the domain into the "right" subdomains. Many mathematicians, including Terry Tao, have suggested that using AI tools to find the right decompositions can be very useful for research-level asymptotic analysis. In this paper, we show that our framework LLM+CAS turns out to be remarkably effective at proposing such decompositions via a combination of a frontier LLM and a CAS. More precisely, we use an LLM to suggest domain decomposition, and a CAS (such as Mathematica) that provides a verification of each piece axiomatically. Using this loop, we answer a question posed by Terence Tao: whether LLMs coupled with a verifier can be used to help prove intricate asymptotic inequalities. More broadly, we show how AI can move beyond contest math towards research-level tools for professional mathematicians.

Robustness of deep learning classification to adversarial input on GPUs: asynchronous parallel accumulation is a source of vulnerability

The ability of machine learning (ML) classification models to resist small, targeted input perturbations - known as adversarial attacks - is a key measure of their safety and reliability. We show that floating-point non associativity (FPNA) coupled with asynchronous parallel programming on GPUs is sufficient to result in misclassification, without any perturbation to the input. Additionally, we show this misclassification is particularly significant for inputs close to the decision boundary and that standard adversarial robustness results may be overestimated up to 4.6% when not considering machine-level details. We first study a linear classifier, before focusing on standard Graph Neural Network (GNN) architectures and datasets. We present a novel black-box attack using Bayesian optimization to determine external workloads that bias the output of reductions on GPUs and reliably lead to misclassification. Motivated by these results, we present a new learnable permutation (LP) gradient-based approach, to learn floating point operation orderings that lead to misclassifications, making the assumption that any reduction or permutation ordering is possible. This LP approach provides a worst-case estimate in a computationally efficient manner, avoiding the need to run identical experiments tens of thousands of times over a potentially large set of possible GPU states or architectures. Finally, we investigate parallel reduction ordering across different GPU architectures for a reduction under three conditions: (1) executing external background workloads, (2) utilizing multi-GPU virtualization, and (3) applying power capping. Our results demonstrate that parallel reduction ordering varies significantly across architectures under the first two conditions. The results and methods developed here can help to include machine-level considerations into adversarial robustness assessments.

LLMStinger: Jailbreaking LLMs using RL fine-tuned LLMs

We introduce LLMStinger, a novel approach that leverages Large Language Models (LLMs) to automatically generate adversarial suffixes for jailbreak attacks. Unlike traditional methods, which require complex prompt engineering or white-box access, LLMStinger uses a reinforcement learning (RL) loop to fine-tune an attacker LLM, generating new suffixes based on existing attacks for harmful questions from the HarmBench benchmark. Our method significantly outperforms existing red-teaming approaches (we compared against 15 of the latest methods), achieving a +57.2% improvement in Attack Success Rate (ASR) on LLaMA2-7B-chat and a +50.3% ASR increase on Claude 2, both models known for their extensive safety measures. Additionally, we achieved a 94.97% ASR on GPT-3.5 and 99.4% on Gemma-2B-it, demonstrating the robustness and adaptability of LLMStinger across open and closed-source models.

Can Transformers Reason Logically? A Study in SAT Solving

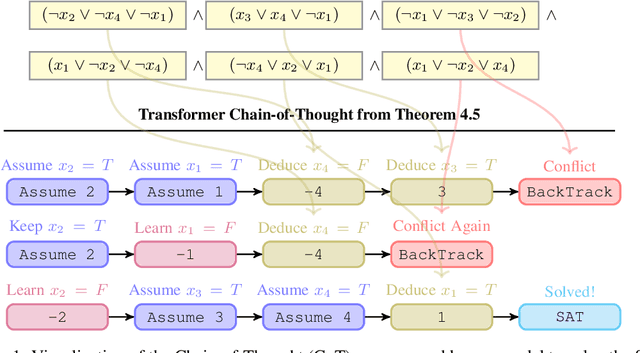
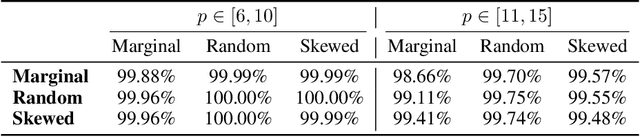
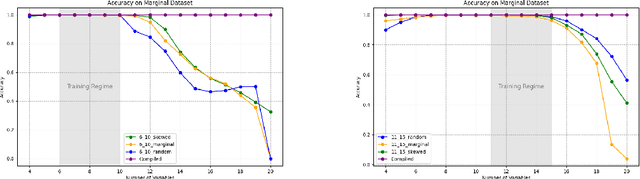
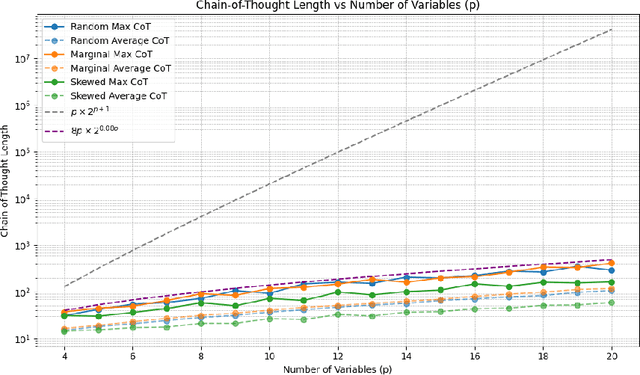
We theoretically and empirically study the logical reasoning capabilities of LLMs in the context of the Boolean satisfiability (SAT) problem. First, we construct a decoder-only Transformer that can solve SAT using backtracking and deduction via Chain-of-Thought (CoT). We prove its correctness by showing trace equivalence to the well-known DPLL SAT-solving algorithm. Second, to support the implementation of this abstract construction, we design a compiler $\texttt{PARAT}$ that takes as input a procedural specification and outputs a transformer model implementing this specification. Third, rather than $\textit{programming}$ a transformer to reason, we evaluate empirically whether it can be $\textit{trained}$ to do so by learning directly from algorithmic traces ("reasoning paths") of the DPLL algorithm.

RLSF: Reinforcement Learning via Symbolic Feedback

In recent years, large language models (LLMs) have had a dramatic impact on various sub-fields of AI, most notably on natural language understanding tasks. However, there is widespread agreement that the logical reasoning capabilities of contemporary LLMs are, at best, fragmentary (i.e., may work well on some problem instances but fail dramatically on others). While traditional LLM fine-tuning approaches (e.g., those that use human feedback) do address this problem to some degree, they suffer from many issues, including unsound black-box reward models, difficulties in collecting preference data, and sparse scalar reward values. To address these challenges, we propose a new training/fine-tuning paradigm we refer to as Reinforcement Learning via Symbolic Feedback (RLSF), which is aimed at enhancing the reasoning capabilities of LLMs. In the RLSF setting, the LLM that is being trained/fine-tuned is considered as the RL agent, while the environment is allowed access to reasoning or domain knowledge tools (e.g., solvers, algebra systems). Crucially, in RLSF, these reasoning tools can provide feedback to the LLMs via poly-sized certificates (e.g., proofs), that characterize errors in the LLM-generated object with respect to some correctness specification. The ability of RLSF-based training/fine-tuning to leverage certificate-generating symbolic tools enables sound fine-grained (token-level) reward signals to LLMs, and thus addresses the limitations of traditional reward models mentioned above. Via extensive evaluations, we show that our RLSF-based fine-tuning of LLMs outperforms traditional approaches on two different applications, namely, program synthesis from natural language pseudo-code to programming language (C++) and solving the Game of 24.

A Reinforcement Learning based Reset Policy for CDCL SAT Solvers

Restart policy is an important technique used in modern Conflict-Driven Clause Learning (CDCL) solvers, wherein some parts of the solver state are erased at certain intervals during the run of the solver. In most solvers, variable activities are preserved across restart boundaries, resulting in solvers continuing to search parts of the assignment tree that are not far from the one immediately prior to a restart. To enable the solver to search possibly "distant" parts of the assignment tree, we study the effect of resets, a variant of restarts which not only erases the assignment trail, but also randomizes the activity scores of the variables of the input formula after reset, thus potentially enabling a better global exploration of the search space. In this paper, we model the problem of whether to trigger reset as a multi-armed bandit (MAB) problem, and propose two reinforcement learning (RL) based adaptive reset policies using the Upper Confidence Bound (UCB) and Thompson sampling algorithms. These two algorithms balance the exploration-exploitation tradeoff by adaptively choosing arms (reset vs. no reset) based on their estimated rewards during the solver's run. We implement our reset policies in four baseline SOTA CDCL solvers and compare the baselines against the reset versions on Satcoin benchmarks and SAT Competition instances. Our results show that RL-based reset versions outperform the corresponding baseline solvers on both Satcoin and the SAT competition instances, suggesting that our RL policy helps to dynamically and profitably adapt the reset frequency for any given input instance. We also introduce the concept of a partial reset, where at least a constant number of variable activities are retained across reset boundaries. Building on previous results, we show that there is an exponential separation between O(1) vs. $\Omega(n)$-length partial resets.

Layered and Staged Monte Carlo Tree Search for SMT Strategy Synthesis

Modern SMT solvers, such as Z3, offer user-controllable strategies, enabling users to tailor them for their unique set of instances, thus dramatically enhancing solver performance for their use case. However, this approach of strategy customization presents a significant challenge: handcrafting an optimized strategy for a class of SMT instances remains a complex and demanding task for both solver developers and users alike. In this paper, we address this problem of automatic SMT strategy synthesis via a novel Monte Carlo Tree Search (MCTS) based method. Our method treats strategy synthesis as a sequential decision-making process, whose search tree corresponds to the strategy space, and employs MCTS to navigate this vast search space. The key innovations that enable our method to identify effective strategies, while keeping costs low, are the ideas of layered and staged MCTS search. These novel approaches allow for a deeper and more efficient exploration of the strategy space, enabling us to synthesize more effective strategies than the default ones in state-of-the-art (SOTA) SMT solvers. We implement our method, dubbed Z3alpha, as part of the Z3 SMT solver. Through extensive evaluations across 6 important SMT logics, Z3alpha demonstrates superior performance compared to the SOTA synthesis tool FastSMT, the default Z3 solver, and the CVC5 solver on most benchmarks. Remarkably, on a challenging QF_BV benchmark set, Z3alpha solves 42.7% more instances than the default strategy in the Z3 SMT solver.

AlphaMapleSAT: An MCTS-based Cube-and-Conquer SAT Solver for Hard Combinatorial Problems

This paper introduces AlphaMapleSAT, a novel Monte Carlo Tree Search (MCTS) based Cube-and-Conquer (CnC) SAT solving method aimed at efficiently solving challenging combinatorial problems. Despite the tremendous success of CnC solvers in solving a variety of hard combinatorial problems, the lookahead cubing techniques at the heart of CnC have not evolved much for many years. Part of the reason is the sheer difficulty of coming up with new cubing techniques that are both low-cost and effective in partitioning input formulas into sub-formulas, such that the overall runtime is minimized. Lookahead cubing techniques used by current state-of-the-art CnC solvers, such as March, keep their cubing costs low by constraining the search for the optimal splitting variables. By contrast, our key innovation is a deductively-driven MCTS-based lookahead cubing technique, that performs a deeper heuristic search to find effective cubes, while keeping the cubing cost low. We perform an extensive comparison of AlphaMapleSAT against the March CnC solver on challenging combinatorial problems such as the minimum Kochen-Specker and Ramsey problems. We also perform ablation studies to verify the efficacy of the MCTS heuristic search for the cubing problem. Results show up to 2.3x speedup in parallel (and up to 27x in sequential) elapsed real time.