SwiReasoning: Switch-Thinking in Latent and Explicit for Pareto-Superior Reasoning LLMs

Recent work shows that, beyond discrete reasoning through explicit chain-of-thought steps, which are limited by the boundaries of natural languages, large language models (LLMs) can also reason continuously in latent space, allowing richer information per step and thereby improving token efficiency. Despite this promise, latent reasoning still faces two challenges, especially in training-free settings: 1) purely latent reasoning broadens the search distribution by maintaining multiple implicit paths, which diffuses probability mass, introduces noise, and impedes convergence to a single high-confidence solution, thereby hurting accuracy; and 2) overthinking persists even without explicit text, wasting tokens and degrading efficiency. To address these issues, we introduce SwiReasoning, a training-free framework for LLM reasoning which features two key innovations: 1) SwiReasoning dynamically switches between explicit and latent reasoning, guided by block-wise confidence estimated from entropy trends in next-token distributions, to balance exploration and exploitation and promote timely convergence. 2) By limiting the maximum number of thinking-block switches, SwiReasoning curbs overthinking and improves token efficiency across varying problem difficulties. On widely used mathematics and STEM benchmarks, SwiReasoning consistently improves average accuracy by 1.5%-2.8% across reasoning LLMs of different model families and scales. Furthermore, under constrained budgets, SwiReasoning improves average token efficiency by 56%-79%, with larger gains as budgets tighten.

Can Transformers Reason Logically? A Study in SAT Solving

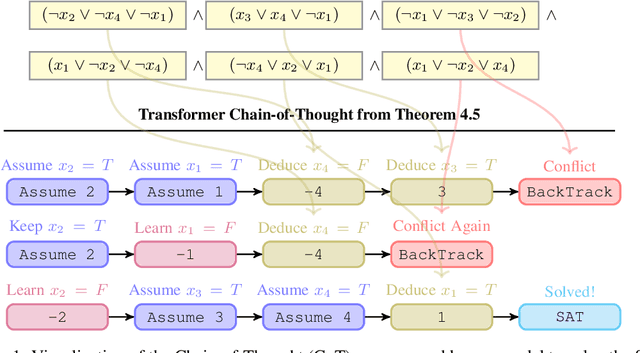
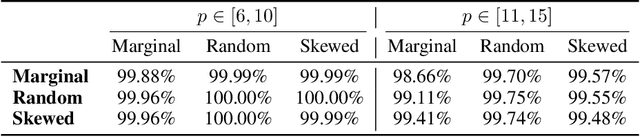
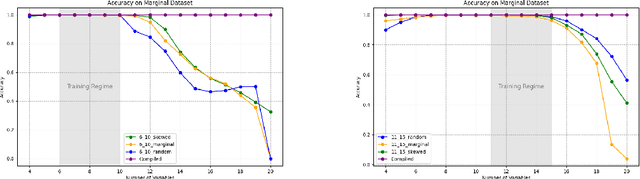
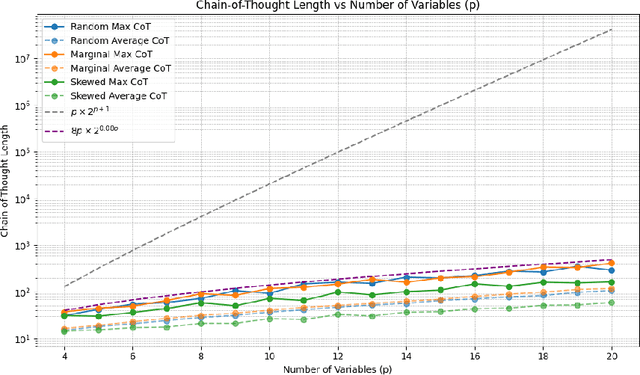
We theoretically and empirically study the logical reasoning capabilities of LLMs in the context of the Boolean satisfiability (SAT) problem. First, we construct a decoder-only Transformer that can solve SAT using backtracking and deduction via Chain-of-Thought (CoT). We prove its correctness by showing trace equivalence to the well-known DPLL SAT-solving algorithm. Second, to support the implementation of this abstract construction, we design a compiler $\texttt{PARAT}$ that takes as input a procedural specification and outputs a transformer model implementing this specification. Third, rather than $\textit{programming}$ a transformer to reason, we evaluate empirically whether it can be $\textit{trained}$ to do so by learning directly from algorithmic traces ("reasoning paths") of the DPLL algorithm.

Towards Understanding Neural Collapse: The Effects of Batch Normalization and Weight Decay

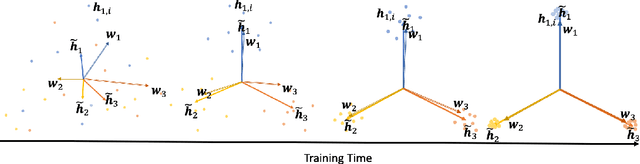
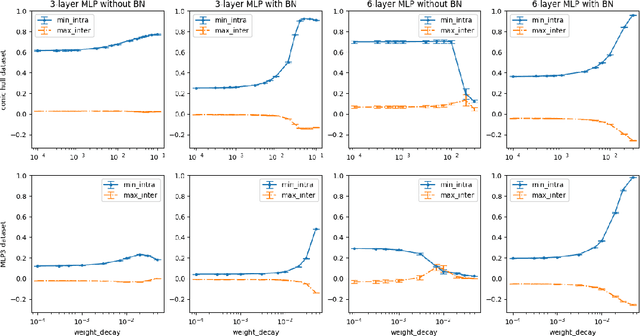
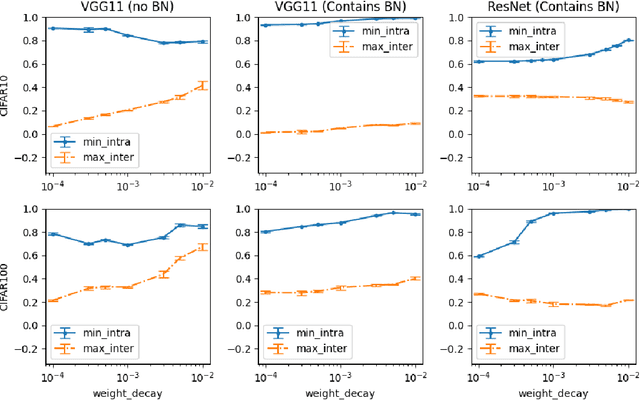
Neural Collapse (NC) is a geometric structure recently observed in the final layer of neural network classifiers. In this paper, we investigate the interrelationships between batch normalization (BN), weight decay, and proximity to the NC structure. Our work introduces the geometrically intuitive intra-class and inter-class cosine similarity measure, which encapsulates multiple core aspects of NC. Leveraging this measure, we establish theoretical guarantees for the emergence of NC under the influence of last-layer BN and weight decay, specifically in scenarios where the regularized cross-entropy loss is near-optimal. Experimental evidence substantiates our theoretical findings, revealing a pronounced occurrence of NC in models incorporating BN and appropriate weight-decay values. This combination of theoretical and empirical insights suggests a greatly influential role of BN and weight decay in the emergence of NC.