StructComp: Substituting propagation with Structural Compression in Training Graph Contrastive Learning

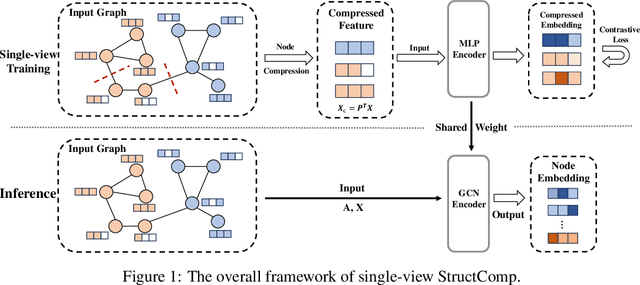
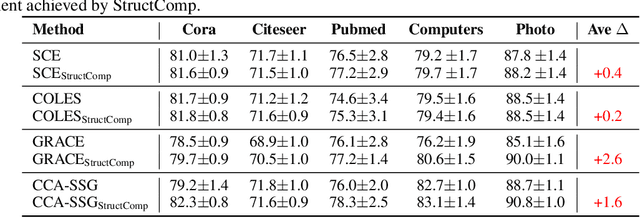
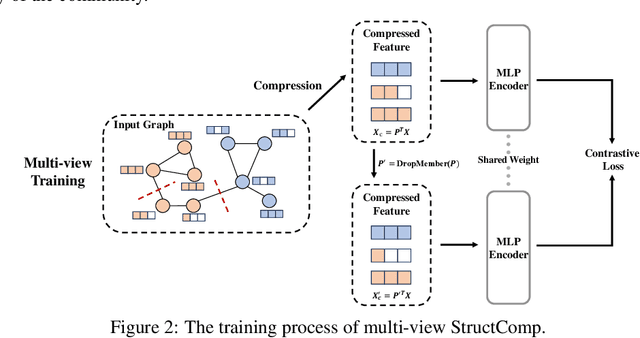
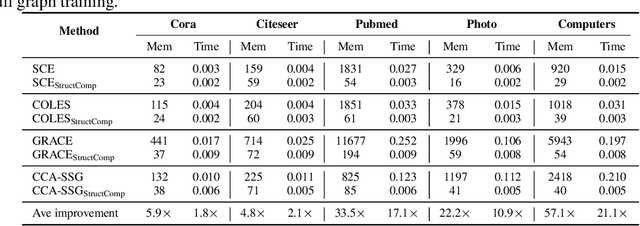
Graph contrastive learning (GCL) has become a powerful tool for learning graph data, but its scalability remains a significant challenge. In this work, we propose a simple yet effective training framework called Structural Compression (StructComp) to address this issue. Inspired by a sparse low-rank approximation on the diffusion matrix, StructComp trains the encoder with the compressed nodes. This allows the encoder not to perform any message passing during the training stage, and significantly reduces the number of sample pairs in the contrastive loss. We theoretically prove that the original GCL loss can be approximated with the contrastive loss computed by StructComp. Moreover, StructComp can be regarded as an additional regularization term for GCL models, resulting in a more robust encoder. Empirical studies on seven benchmark datasets show that StructComp greatly reduces the time and memory consumption while improving model performance compared to the vanilla GCL models and scalable training methods.

Contrastive Moments: Unsupervised Halfspace Learning in Polynomial Time

We give a polynomial-time algorithm for learning high-dimensional halfspaces with margins in $d$-dimensional space to within desired TV distance when the ambient distribution is an unknown affine transformation of the $d$-fold product of an (unknown) symmetric one-dimensional logconcave distribution, and the halfspace is introduced by deleting at least an $\epsilon$ fraction of the data in one of the component distributions. Notably, our algorithm does not need labels and establishes the unique (and efficient) identifiability of the hidden halfspace under this distributional assumption. The sample and time complexity of the algorithm are polynomial in the dimension and $1/\epsilon$. The algorithm uses only the first two moments of suitable re-weightings of the empirical distribution, which we call contrastive moments; its analysis uses classical facts about generalized Dirichlet polynomials and relies crucially on a new monotonicity property of the moment ratio of truncations of logconcave distributions. Such algorithms, based only on first and second moments were suggested in earlier work, but hitherto eluded rigorous guarantees. Prior work addressed the special case when the underlying distribution is Gaussian via Non-Gaussian Component Analysis. We improve on this by providing polytime guarantees based on Total Variation (TV) distance, in place of existing moment-bound guarantees that can be super-polynomial. Our work is also the first to go beyond Gaussians in this setting.

Towards Understanding Neural Collapse: The Effects of Batch Normalization and Weight Decay

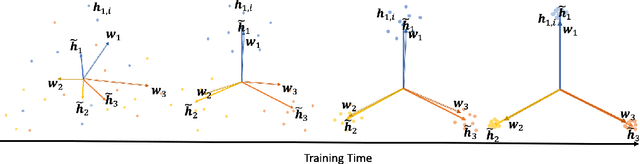
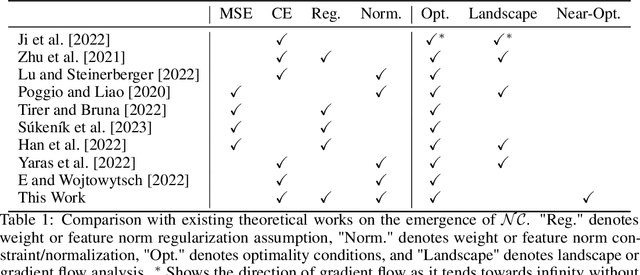
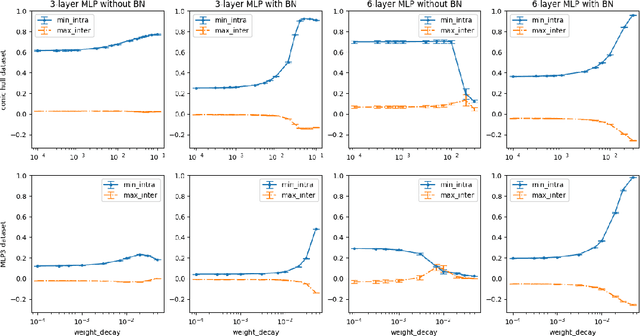
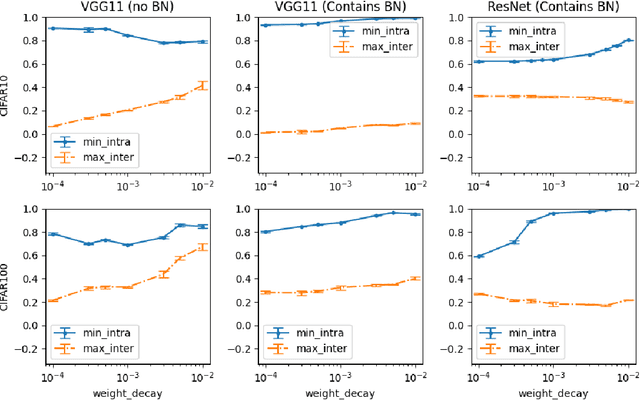
Neural Collapse (NC) is a geometric structure recently observed in the final layer of neural network classifiers. In this paper, we investigate the interrelationships between batch normalization (BN), weight decay, and proximity to the NC structure. Our work introduces the geometrically intuitive intra-class and inter-class cosine similarity measure, which encapsulates multiple core aspects of NC. Leveraging this measure, we establish theoretical guarantees for the emergence of NC under the influence of last-layer BN and weight decay, specifically in scenarios where the regularized cross-entropy loss is near-optimal. Experimental evidence substantiates our theoretical findings, revealing a pronounced occurrence of NC in models incorporating BN and appropriate weight-decay values. This combination of theoretical and empirical insights suggests a greatly influential role of BN and weight decay in the emergence of NC.

Graph-Level Embedding for Time-Evolving Graphs

Graph representation learning (also known as network embedding) has been extensively researched with varying levels of granularity, ranging from nodes to graphs. While most prior work in this area focuses on node-level representation, limited research has been conducted on graph-level embedding, particularly for dynamic or temporal networks. However, learning low-dimensional graph-level representations for dynamic networks is critical for various downstream graph retrieval tasks such as temporal graph similarity ranking, temporal graph isomorphism, and anomaly detection. In this paper, we present a novel method for temporal graph-level embedding that addresses this gap. Our approach involves constructing a multilayer graph and using a modified random walk with temporal backtracking to generate temporal contexts for the graph's nodes. We then train a "document-level" language model on these contexts to generate graph-level embeddings. We evaluate our proposed model on five publicly available datasets for the task of temporal graph similarity ranking, and our model outperforms baseline methods. Our experimental results demonstrate the effectiveness of our method in generating graph-level embeddings for dynamic networks.

Provable Lifelong Learning of Representations

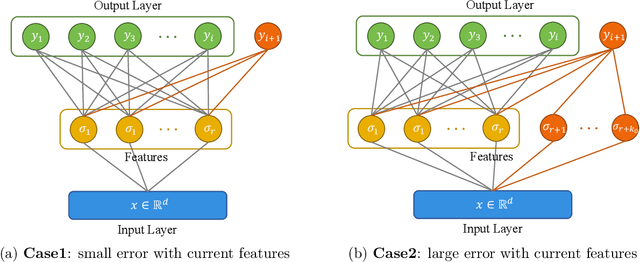
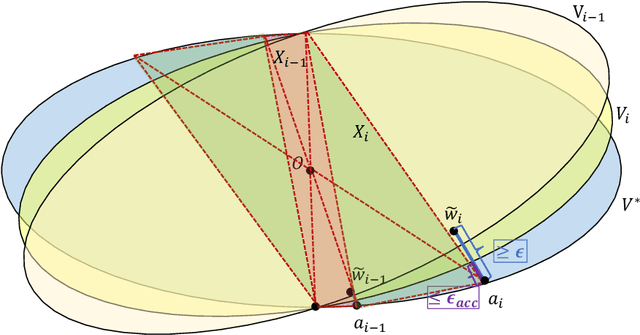
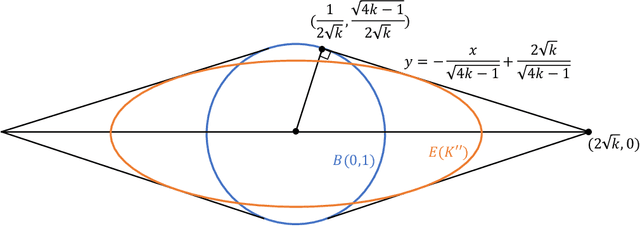
In lifelong learning, the tasks (or classes) to be learned arrive sequentially over time in arbitrary order. During training, knowledge from previous tasks can be captured and transferred to subsequent ones to improve sample efficiency. We consider the setting where all target tasks can be represented in the span of a small number of unknown linear or nonlinear features of the input data. We propose a provable lifelong learning algorithm that maintains and refines the internal feature representation. We prove that for any desired accuracy on all tasks, the dimension of the representation remains close to that of the underlying representation. The resulting sample complexity improves significantly on existing bounds. In the setting of linear features, our algorithm is provably efficient and the sample complexity for input dimension $d$, $m$ tasks with $k$ features up to error $\epsilon$ is $\tilde{O}(dk^{1.5}/\epsilon+km/\epsilon)$. We also prove a matching lower bound for any lifelong learning algorithm that uses a single task learner as a black box. Finally, we complement our analysis with an empirical study.

Graph Embedding via Diffusion-Wavelets-Based Node Feature Distribution Characterization

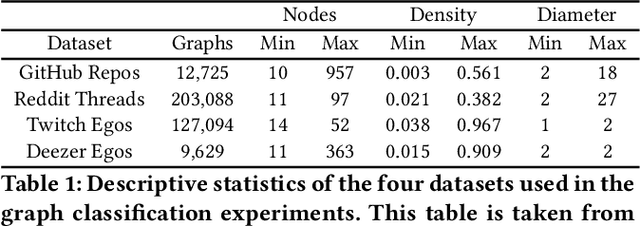
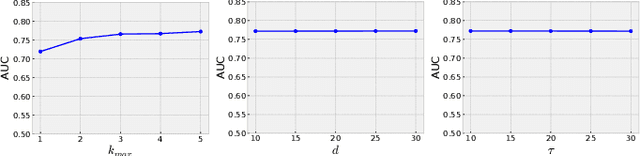
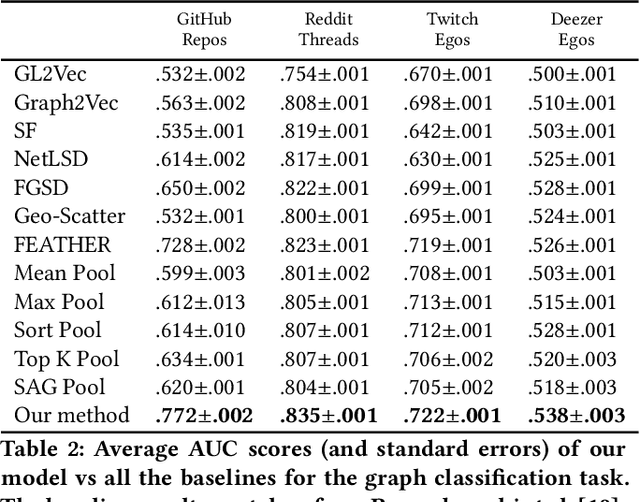
Recent years have seen a rise in the development of representational learning methods for graph data. Most of these methods, however, focus on node-level representation learning at various scales (e.g., microscopic, mesoscopic, and macroscopic node embedding). In comparison, methods for representation learning on whole graphs are currently relatively sparse. In this paper, we propose a novel unsupervised whole graph embedding method. Our method uses spectral graph wavelets to capture topological similarities on each k-hop sub-graph between nodes and uses them to learn embeddings for the whole graph. We evaluate our method against 12 well-known baselines on 4 real-world datasets and show that our method achieves the best performance across all experiments, outperforming the current state-of-the-art by a considerable margin.