AlphaMapleSAT: An MCTS-based Cube-and-Conquer SAT Solver for Hard Combinatorial Problems

This paper introduces AlphaMapleSAT, a novel Monte Carlo Tree Search (MCTS) based Cube-and-Conquer (CnC) SAT solving method aimed at efficiently solving challenging combinatorial problems. Despite the tremendous success of CnC solvers in solving a variety of hard combinatorial problems, the lookahead cubing techniques at the heart of CnC have not evolved much for many years. Part of the reason is the sheer difficulty of coming up with new cubing techniques that are both low-cost and effective in partitioning input formulas into sub-formulas, such that the overall runtime is minimized. Lookahead cubing techniques used by current state-of-the-art CnC solvers, such as March, keep their cubing costs low by constraining the search for the optimal splitting variables. By contrast, our key innovation is a deductively-driven MCTS-based lookahead cubing technique, that performs a deeper heuristic search to find effective cubes, while keeping the cubing cost low. We perform an extensive comparison of AlphaMapleSAT against the March CnC solver on challenging combinatorial problems such as the minimum Kochen-Specker and Ramsey problems. We also perform ablation studies to verify the efficacy of the MCTS heuristic search for the cubing problem. Results show up to 2.3x speedup in parallel (and up to 27x in sequential) elapsed real time.

Integer and Constraint Programming Revisited for Mutually Orthogonal Latin Squares

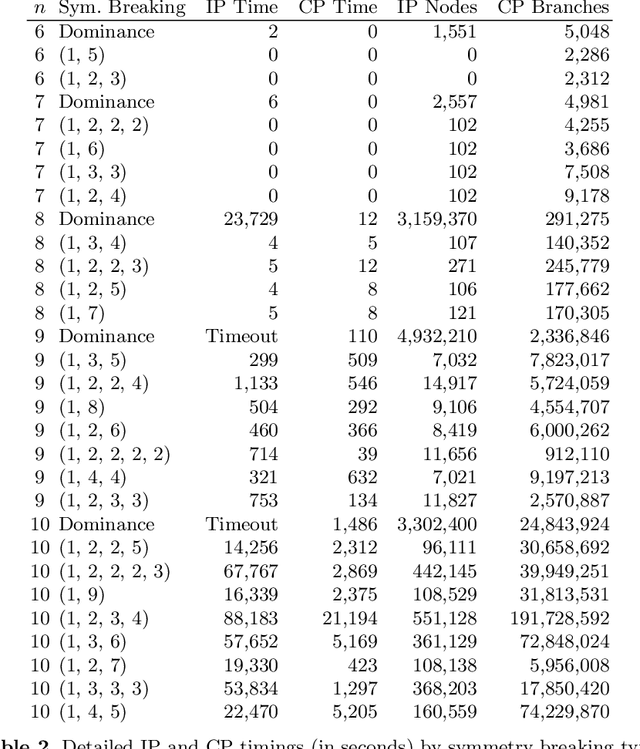
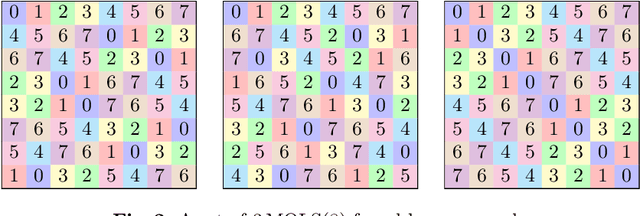
In this paper we provide results on using integer programming (IP) and constraint programming (CP) to search for sets of mutually orthogonal latin squares (MOLS). Both programming paradigms have previously successfully been used to search for MOLS, but solvers for IP and CP solvers have significantly improved in recent years and data on how modern IP and CP solvers perform on the MOLS problem is lacking. Using state-of-the-art solvers as black boxes we were able to quickly find pairs of MOLS (or prove their nonexistence) in all orders up to ten. Moreover, we improve the effectiveness of the solvers by formulating an extended symmetry breaking method as well as an improvement to the straightforward CP encoding. We also analyze the effectiveness of using CP and IP solvers to search for triples of MOLS, compare our timings to those which have been previously published, and estimate the running time of using this approach to resolve the longstanding open problem of determining the existence of a triple of MOLS of order ten.

A SAT-based Resolution of Lam's Problem

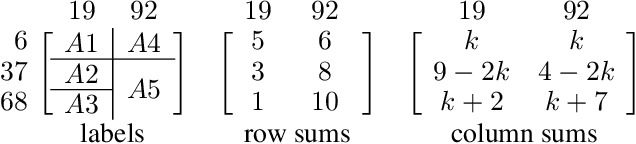
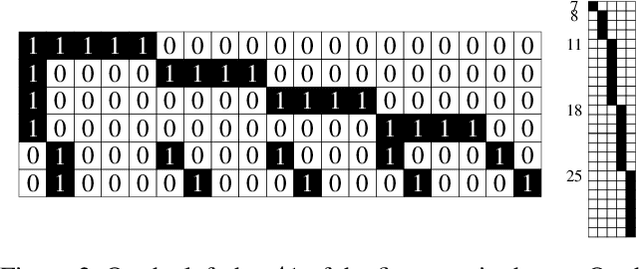
In 1989, computer searches by Lam, Thiel, and Swiercz experimentally resolved Lam's problem from projective geometry$\unicode{x2014}$the long-standing problem of determining if a projective plane of order ten exists. Both the original search and an independent verification in 2011 discovered no such projective plane. However, these searches were each performed using highly specialized custom-written code and did not produce nonexistence certificates. In this paper, we resolve Lam's problem by translating the problem into Boolean logic and use satisfiability (SAT) solvers to produce nonexistence certificates that can be verified by a third party. Our work uncovered consistency issues in both previous searches$\unicode{x2014}$highlighting the difficulty of relying on special-purpose search code for nonexistence results.

Effective problem solving using SAT solvers

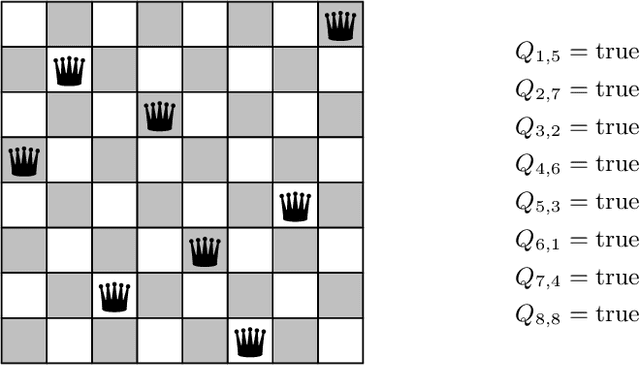
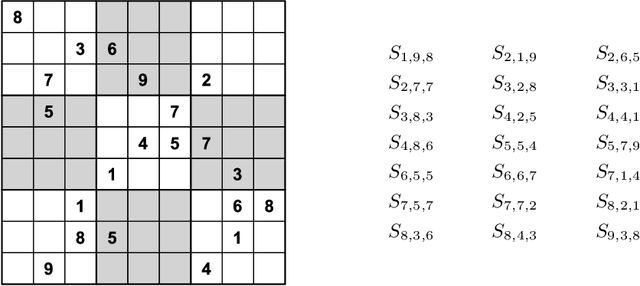
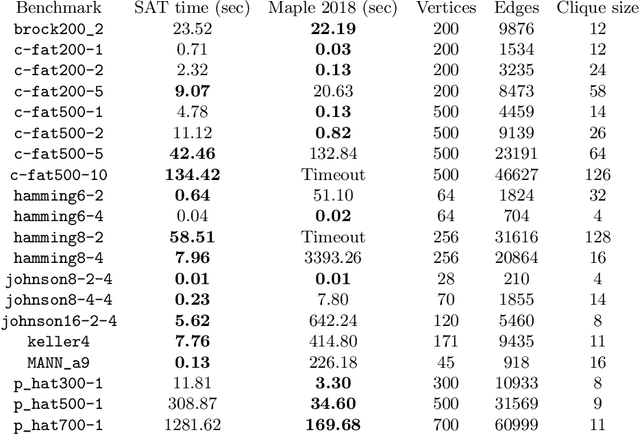
In this article we demonstrate how to solve a variety of problems and puzzles using the built-in SAT solver of the computer algebra system Maple. Once the problems have been encoded into Boolean logic, solutions can be found (or shown to not exist) automatically, without the need to implement any search algorithm. In particular, we describe how to solve the $n$-queens problem, how to generate and solve Sudoku puzzles, how to solve logic puzzles like the Einstein riddle, how to solve the 15-puzzle, how to solve the maximum clique problem, and finding Graeco-Latin squares.