High-Fidelity, Customizable Force Sensing for the Wearable Human-Robot Interface

Mechanically characterizing the human-machine interface is essential to understanding user behavior and optimizing wearable robot performance. This interface has been challenging to sensorize due to manufacturing complexity and non-linear sensor responses. Here, we measure human limb-device interaction via fluidic innervation, creating a 3D-printed silicone pad with embedded air channels to measure forces. As forces are applied to the pad, the air channels compress, resulting in a pressure change measurable by off-the-shelf pressure transducers. We demonstrate in benchtop testing that pad pressure is highly linearly related to applied force ($R^2 = 0.998$). This is confirmed with clinical dynamometer correlations with isometric knee torque, where above-knee pressure was highly correlated with flexion torque ($R^2 = 0.95$), while below-knee pressure was highly correlated with extension torque ($R^2 = 0.75$). We build on these idealized settings to test pad performance in more unconstrained settings. We place the pad over \textit{biceps brachii} during cyclic curls and stepwise isometric holds, observing a correlation between pressure and elbow angle. Finally, we integrated the sensor into the strap of a lower-extremity robotic exoskeleton and recorded pad pressure during repeated squats with the device unpowered. Pad pressure tracked squat phase and overall task dynamics consistently. Overall, our preliminary results suggest fluidic innervation is a readily customizable sensing modality with high signal-to-noise ratio and temporal resolution for capturing human-machine mechanical interaction. In the long-term, this modality may provide an alternative real-time sensing input to control / optimize wearable robotic systems and to capture user function during device use.

Integer and Constraint Programming Revisited for Mutually Orthogonal Latin Squares

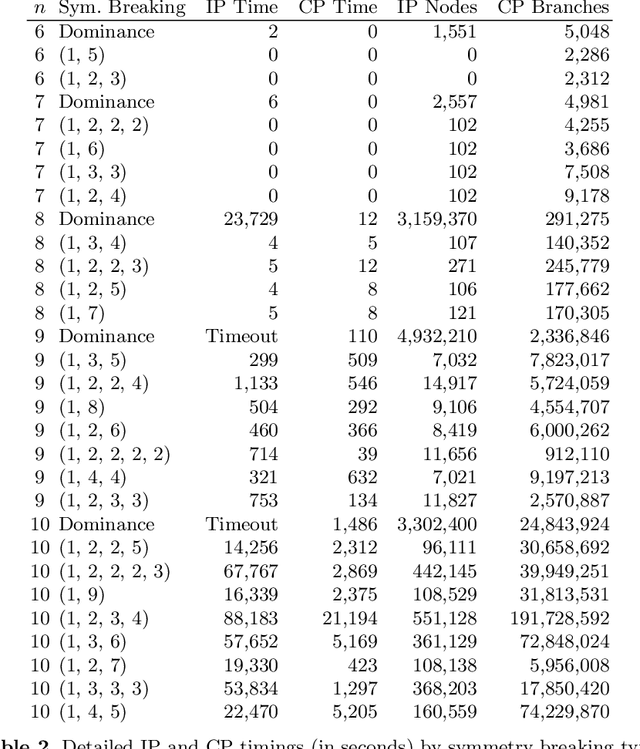
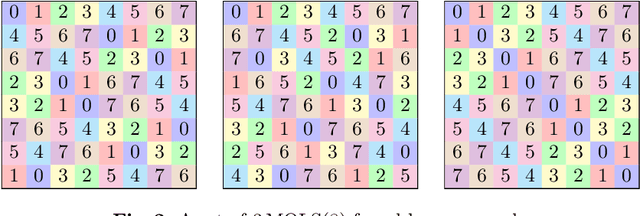
In this paper we provide results on using integer programming (IP) and constraint programming (CP) to search for sets of mutually orthogonal latin squares (MOLS). Both programming paradigms have previously successfully been used to search for MOLS, but solvers for IP and CP solvers have significantly improved in recent years and data on how modern IP and CP solvers perform on the MOLS problem is lacking. Using state-of-the-art solvers as black boxes we were able to quickly find pairs of MOLS (or prove their nonexistence) in all orders up to ten. Moreover, we improve the effectiveness of the solvers by formulating an extended symmetry breaking method as well as an improvement to the straightforward CP encoding. We also analyze the effectiveness of using CP and IP solvers to search for triples of MOLS, compare our timings to those which have been previously published, and estimate the running time of using this approach to resolve the longstanding open problem of determining the existence of a triple of MOLS of order ten.