Layered and Staged Monte Carlo Tree Search for SMT Strategy Synthesis

Modern SMT solvers, such as Z3, offer user-controllable strategies, enabling users to tailor them for their unique set of instances, thus dramatically enhancing solver performance for their use case. However, this approach of strategy customization presents a significant challenge: handcrafting an optimized strategy for a class of SMT instances remains a complex and demanding task for both solver developers and users alike. In this paper, we address this problem of automatic SMT strategy synthesis via a novel Monte Carlo Tree Search (MCTS) based method. Our method treats strategy synthesis as a sequential decision-making process, whose search tree corresponds to the strategy space, and employs MCTS to navigate this vast search space. The key innovations that enable our method to identify effective strategies, while keeping costs low, are the ideas of layered and staged MCTS search. These novel approaches allow for a deeper and more efficient exploration of the strategy space, enabling us to synthesize more effective strategies than the default ones in state-of-the-art (SOTA) SMT solvers. We implement our method, dubbed Z3alpha, as part of the Z3 SMT solver. Through extensive evaluations across 6 important SMT logics, Z3alpha demonstrates superior performance compared to the SOTA synthesis tool FastSMT, the default Z3 solver, and the CVC5 solver on most benchmarks. Remarkably, on a challenging QF_BV benchmark set, Z3alpha solves 42.7% more instances than the default strategy in the Z3 SMT solver.

String Theories involving Regular Membership Predicates: From Practice to Theory and Back

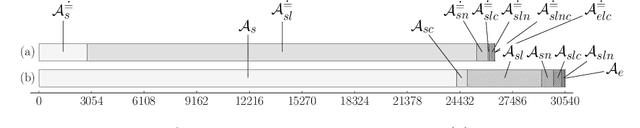
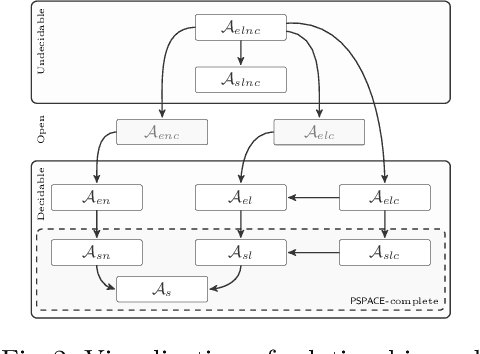
Widespread use of string solvers in formal analysis of string-heavy programs has led to a growing demand for more efficient and reliable techniques which can be applied in this context, especially for real-world cases. Designing an algorithm for the (generally undecidable) satisfiability problem for systems of string constraints requires a thorough understanding of the structure of constraints present in the targeted cases. In this paper, we investigate benchmarks presented in the literature containing regular expression membership predicates, extract different first order logic theories, and prove their decidability, resp. undecidability. Notably, the most common theories in real-world benchmarks are PSPACE-complete and directly lead to the implementation of a more efficient algorithm to solving string constraints.