String Theories involving Regular Membership Predicates: From Practice to Theory and Back

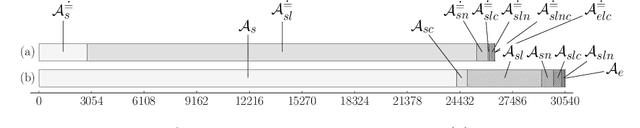
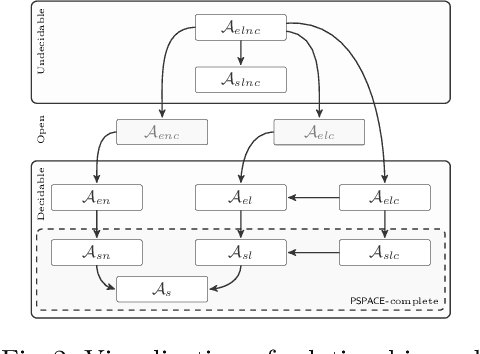
Widespread use of string solvers in formal analysis of string-heavy programs has led to a growing demand for more efficient and reliable techniques which can be applied in this context, especially for real-world cases. Designing an algorithm for the (generally undecidable) satisfiability problem for systems of string constraints requires a thorough understanding of the structure of constraints present in the targeted cases. In this paper, we investigate benchmarks presented in the literature containing regular expression membership predicates, extract different first order logic theories, and prove their decidability, resp. undecidability. Notably, the most common theories in real-world benchmarks are PSPACE-complete and directly lead to the implementation of a more efficient algorithm to solving string constraints.