Predictive Entropy Search for Multi-objective Bayesian Optimization
Paper and Code
Feb 21, 2016
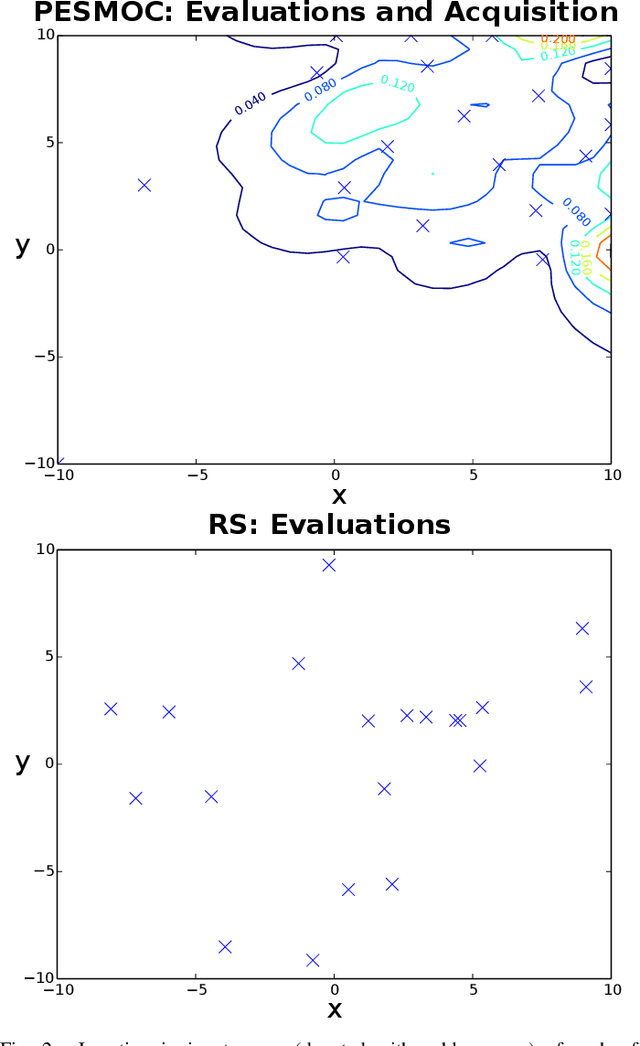
We present PESMO, a Bayesian method for identifying the Pareto set of multi-objective optimization problems, when the functions are expensive to evaluate. The central idea of PESMO is to choose evaluation points so as to maximally reduce the entropy of the posterior distribution over the Pareto set. Critically, the PESMO multi-objective acquisition function can be decomposed as a sum of objective-specific acquisition functions, which enables the algorithm to be used in \emph{decoupled} scenarios in which the objectives can be evaluated separately and perhaps with different costs. This decoupling capability also makes it possible to identify difficult objectives that require more evaluations. PESMO also offers gains in efficiency, as its cost scales linearly with the number of objectives, in comparison to the exponential cost of other methods. We compare PESMO with other related methods for multi-objective Bayesian optimization on synthetic and real-world problems. The results show that PESMO produces better recommendations with a smaller number of evaluations of the objectives, and that a decoupled evaluation can lead to improvements in performance, particularly when the number of objectives is large.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge