Throwing Away Data Improves Worst-Class Error in Imbalanced Classification

Class imbalances pervade classification problems, yet their treatment differs in theory and practice. On the one hand, learning theory instructs us that \emph{more data is better}, as sample size relates inversely to the average test error over the entire data distribution. On the other hand, practitioners have long developed a plethora of tricks to improve the performance of learning machines over imbalanced data. These include data reweighting and subsampling, synthetic construction of additional samples from minority classes, ensembling expensive one-versus all architectures, and tweaking classification losses and thresholds. All of these are efforts to minimize the worst-class error, which is often associated to the minority group in the training data, and finds additional motivation in the robustness, fairness, and out-of-distribution literatures. Here we take on the challenge of developing learning theory able to describe the worst-class error of classifiers over linearly-separable data when fitted either on (i) the full training set, or (ii) a subset where the majority class is subsampled to match in size the minority class. We borrow tools from extreme value theory to show that, under distributions with certain tail properties, \emph{throwing away most data from the majority class leads to better worst-class error}.

Simple data balancing achieves competitive worst-group-accuracy

We study the problem of learning classifiers that perform well across (known or unknown) groups of data. After observing that common worst-group-accuracy datasets suffer from substantial imbalances, we set out to compare state-of-the-art methods to simple balancing of classes and groups by either subsampling or reweighting data. Our results show that these data balancing baselines achieve state-of-the-art-accuracy, while being faster to train and requiring no additional hyper-parameters. In addition, we highlight that access to group information is most critical for model selection purposes, and not so much during training. All in all, our findings beg closer examination of benchmarks and methods for research in worst-group-accuracy optimization.

Out of Distribution Generalization in Machine Learning

Machine learning has achieved tremendous success in a variety of domains in recent years. However, a lot of these success stories have been in places where the training and the testing distributions are extremely similar to each other. In everyday situations when models are tested in slightly different data than they were trained on, ML algorithms can fail spectacularly. This research attempts to formally define this problem, what sets of assumptions are reasonable to make in our data and what kind of guarantees we hope to obtain from them. Then, we focus on a certain class of out of distribution problems, their assumptions, and introduce simple algorithms that follow from these assumptions that are able to provide more reliable generalization. A central topic in the thesis is the strong link between discovering the causal structure of the data, finding features that are reliable (when using them to predict) regardless of their context, and out of distribution generalization.

Linear unit-tests for invariance discovery

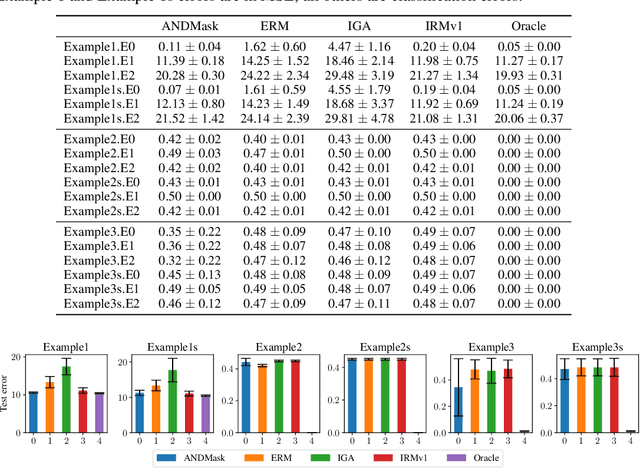
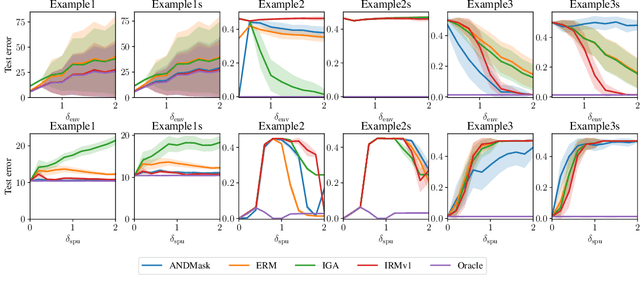
There is an increasing interest in algorithms to learn invariant correlations across training environments. A big share of the current proposals find theoretical support in the causality literature but, how useful are they in practice? The purpose of this note is to propose six linear low-dimensional problems -- unit tests -- to evaluate different types of out-of-distribution generalization in a precise manner. Following initial experiments, none of the three recently proposed alternatives passes all tests. By providing the code to automatically replicate all the results in this manuscript (https://www.github.com/facebookresearch/InvarianceUnitTests), we hope that our unit tests become a standard steppingstone for researchers in out-of-distribution generalization.

Low Distortion Block-Resampling with Spatially Stochastic Networks

We formalize and attack the problem of generating new images from old ones that are as diverse as possible, only allowing them to change without restrictions in certain parts of the image while remaining globally consistent. This encompasses the typical situation found in generative modelling, where we are happy with parts of the generated data, but would like to resample others ("I like this generated castle overall, but this tower looks unrealistic, I would like a new one"). In order to attack this problem we build from the best conditional and unconditional generative models to introduce a new network architecture, training procedure, and algorithm for resampling parts of the image as desired.

Symplectic Recurrent Neural Networks

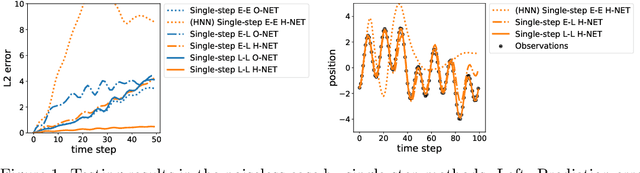
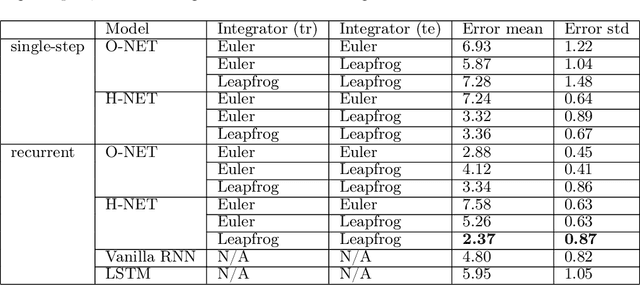
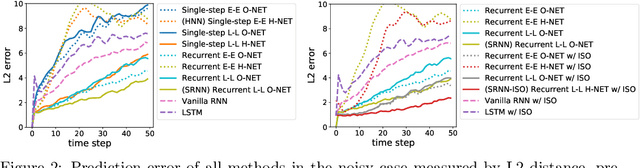
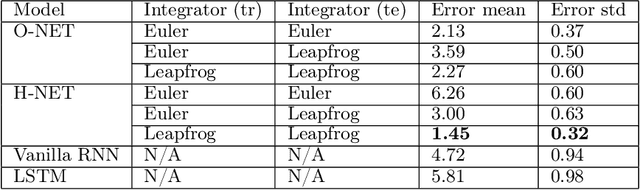
We propose Symplectic Recurrent Neural Networks (SRNNs) as learning algorithms that capture the dynamics of physical systems from observed trajectories. An SRNN models the Hamiltonian function of the system by a neural network and furthermore leverages symplectic integration, multiple-step training and initial state optimization to address the challenging numerical issues associated with Hamiltonian systems. We show SRNNs succeed reliably on complex and noisy Hamiltonian systems. We also show how to augment the SRNN integration scheme in order to handle stiff dynamical systems such as bouncing billiards.

Invariant Risk Minimization

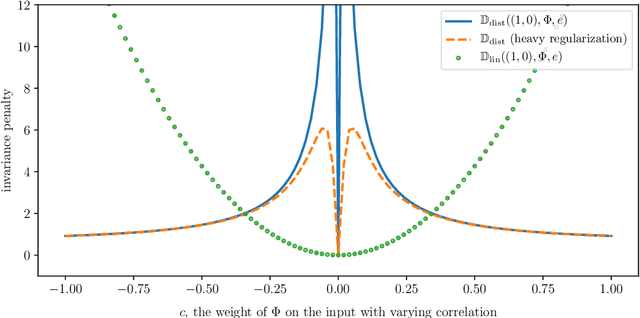
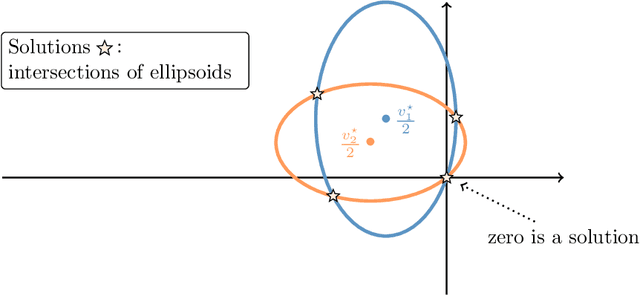
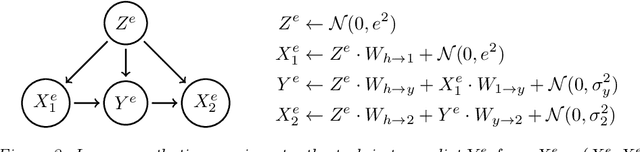
We introduce Invariant Risk Minimization (IRM), a learning paradigm to estimate invariant correlations across multiple training distributions. To achieve this goal, IRM learns a data representation such that the optimal classifier, on top of that data representation, matches for all training distributions. Through theory and experiments, we show how the invariances learned by IRM relate to the causal structures governing the data and enable out-of-distribution generalization.

Geometrical Insights for Implicit Generative Modeling

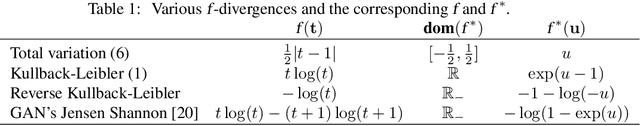
Learning algorithms for implicit generative models can optimize a variety of criteria that measure how the data distribution differs from the implicit model distribution, including the Wasserstein distance, the Energy distance, and the Maximum Mean Discrepancy criterion. A careful look at the geometries induced by these distances on the space of probability measures reveals interesting differences. In particular, we can establish surprising approximate global convergence guarantees for the $1$-Wasserstein distance,even when the parametric generator has a nonconvex parametrization.

Improved Training of Wasserstein GANs

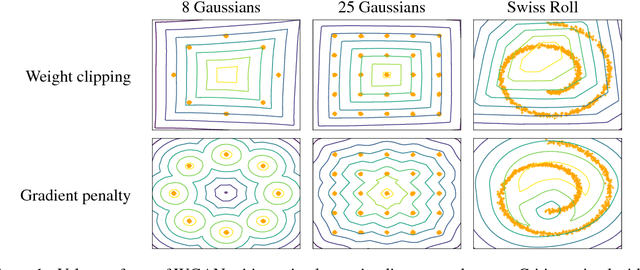
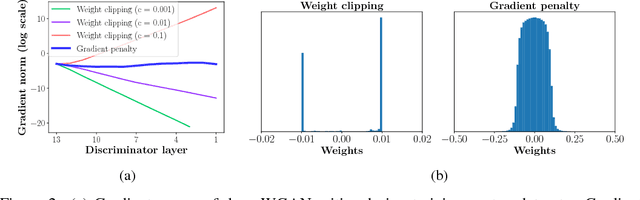
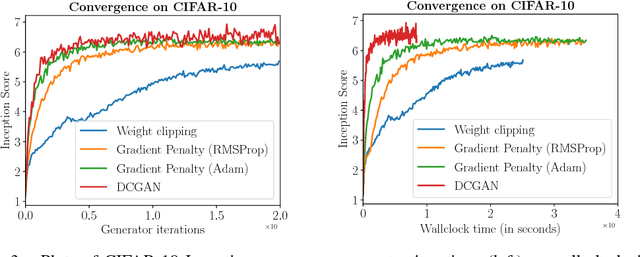
Generative Adversarial Networks (GANs) are powerful generative models, but suffer from training instability. The recently proposed Wasserstein GAN (WGAN) makes progress toward stable training of GANs, but sometimes can still generate only low-quality samples or fail to converge. We find that these problems are often due to the use of weight clipping in WGAN to enforce a Lipschitz constraint on the critic, which can lead to undesired behavior. We propose an alternative to clipping weights: penalize the norm of gradient of the critic with respect to its input. Our proposed method performs better than standard WGAN and enables stable training of a wide variety of GAN architectures with almost no hyperparameter tuning, including 101-layer ResNets and language models over discrete data. We also achieve high quality generations on CIFAR-10 and LSUN bedrooms.

Wasserstein GAN

We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability of learning, get rid of problems like mode collapse, and provide meaningful learning curves useful for debugging and hyperparameter searches. Furthermore, we show that the corresponding optimization problem is sound, and provide extensive theoretical work highlighting the deep connections to other distances between distributions.