Symplectic Recurrent Neural Networks
Paper and Code
Sep 29, 2019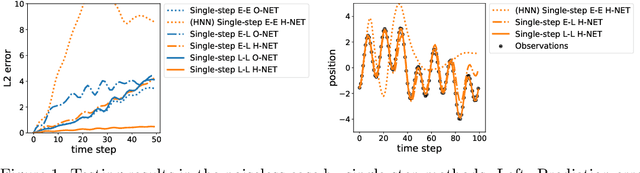
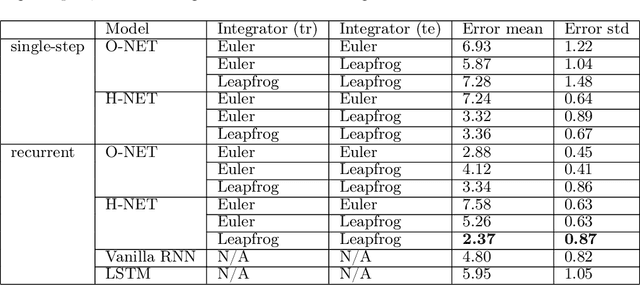
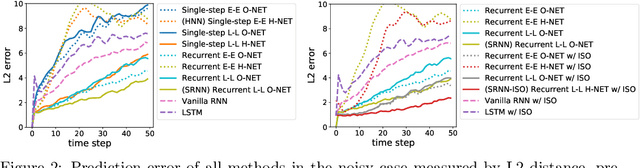
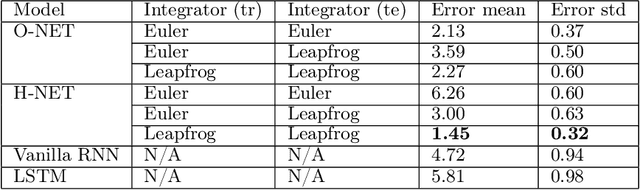
We propose Symplectic Recurrent Neural Networks (SRNNs) as learning algorithms that capture the dynamics of physical systems from observed trajectories. An SRNN models the Hamiltonian function of the system by a neural network and furthermore leverages symplectic integration, multiple-step training and initial state optimization to address the challenging numerical issues associated with Hamiltonian systems. We show SRNNs succeed reliably on complex and noisy Hamiltonian systems. We also show how to augment the SRNN integration scheme in order to handle stiff dynamical systems such as bouncing billiards.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge