Aaron Zweig
Towards Identifiability of Interventional Stochastic Differential Equations
May 21, 2025Abstract:We study identifiability of stochastic differential equation (SDE) models under multiple interventions. Our results give the first provable bounds for unique recovery of SDE parameters given samples from their stationary distributions. We give tight bounds on the number of necessary interventions for linear SDEs, and upper bounds for nonlinear SDEs in the small noise regime. We experimentally validate the recovery of true parameters in synthetic data, and motivated by our theoretical results, demonstrate the advantage of parameterizations with learnable activation functions.
Interpretable Neural ODEs for Gene Regulatory Network Discovery under Perturbations
Jan 05, 2025



Abstract:Modern high-throughput biological datasets with thousands of perturbations provide the opportunity for large-scale discovery of causal graphs that represent the regulatory interactions between genes. Numerous methods have been proposed to infer a directed acyclic graph (DAG) corresponding to the underlying gene regulatory network (GRN) that captures causal gene relationships. However, existing models have restrictive assumptions (e.g. linearity, acyclicity), limited scalability, and/or fail to address the dynamic nature of biological processes such as cellular differentiation. We propose PerturbODE, a novel framework that incorporates biologically informative neural ordinary differential equations (neural ODEs) to model cell state trajectories under perturbations and derive the causal GRN from the neural ODE's parameters. We demonstrate PerturbODE's efficacy in trajectory prediction and GRN inference across simulated and real over-expression datasets.
Symmetric Single Index Learning
Oct 03, 2023
Abstract:Few neural architectures lend themselves to provable learning with gradient based methods. One popular model is the single-index model, in which labels are produced by composing an unknown linear projection with a possibly unknown scalar link function. Learning this model with SGD is relatively well-understood, whereby the so-called information exponent of the link function governs a polynomial sample complexity rate. However, extending this analysis to deeper or more complicated architectures remains challenging. In this work, we consider single index learning in the setting of symmetric neural networks. Under analytic assumptions on the activation and maximum degree assumptions on the link function, we prove that gradient flow recovers the hidden planted direction, represented as a finitely supported vector in the feature space of power sum polynomials. We characterize a notion of information exponent adapted to our setting that controls the efficiency of learning.
On Single Index Models beyond Gaussian Data
Jul 28, 2023Abstract:Sparse high-dimensional functions have arisen as a rich framework to study the behavior of gradient-descent methods using shallow neural networks, showcasing their ability to perform feature learning beyond linear models. Amongst those functions, the simplest are single-index models $f(x) = \phi( x \cdot \theta^*)$, where the labels are generated by an arbitrary non-linear scalar link function $\phi$ applied to an unknown one-dimensional projection $\theta^*$ of the input data. By focusing on Gaussian data, several recent works have built a remarkable picture, where the so-called information exponent (related to the regularity of the link function) controls the required sample complexity. In essence, these tools exploit the stability and spherical symmetry of Gaussian distributions. In this work, building from the framework of \cite{arous2020online}, we explore extensions of this picture beyond the Gaussian setting, where both stability or symmetry might be violated. Focusing on the planted setting where $\phi$ is known, our main results establish that Stochastic Gradient Descent can efficiently recover the unknown direction $\theta^*$ in the high-dimensional regime, under assumptions that extend previous works ~\cite{yehudai2020learning,wu2022learning}.
Towards Antisymmetric Neural Ansatz Separation
Aug 05, 2022


Abstract:We study separations between two fundamental models (or \emph{Ans\"atze}) of antisymmetric functions, that is, functions $f$ of the form $f(x_{\sigma(1)}, \ldots, x_{\sigma(N)}) = \text{sign}(\sigma)f(x_1, \ldots, x_N)$, where $\sigma$ is any permutation. These arise in the context of quantum chemistry, and are the basic modeling tool for wavefunctions of Fermionic systems. Specifically, we consider two popular antisymmetric Ans\"atze: the Slater representation, which leverages the alternating structure of determinants, and the Jastrow ansatz, which augments Slater determinants with a product by an arbitrary symmetric function. We construct an antisymmetric function that can be more efficiently expressed in Jastrow form, yet provably cannot be approximated by Slater determinants unless there are exponentially (in $N^2$) many terms. This represents the first explicit quantitative separation between these two Ans\"atze.
Exponential Separations in Symmetric Neural Networks
Jun 02, 2022
Abstract:In this work we demonstrate a novel separation between symmetric neural network architectures. Specifically, we consider the Relational Network~\parencite{santoro2017simple} architecture as a natural generalization of the DeepSets~\parencite{zaheer2017deep} architecture, and study their representational gap. Under the restriction to analytic activation functions, we construct a symmetric function acting on sets of size $N$ with elements in dimension $D$, which can be efficiently approximated by the former architecture, but provably requires width exponential in $N$ and $D$ for the latter.
A Functional Perspective on Learning Symmetric Functions with Neural Networks
Aug 16, 2020



Abstract:Symmetric functions, which take as input an unordered, fixed-size set, are known to be universally representable by neural networks that enforce permutation invariance. However, these architectures only give guarantees for fixed input sizes, yet in many practical scenarios, such as particle physics, a relevant notion of generalization should include varying the input size. In this paper, we embed symmetric functions (of any size) as functions over probability measures, and study the ability of neural networks defined over this space of measures to represent and learn in that space. By focusing on shallow architectures, we establish approximation and generalization bounds under different choices of regularization (such as RKHS and variation norms), that capture a hierarchy of functional spaces with increasing amount of non-linear learning. The resulting models can be learnt efficiently and enjoy generalization guarantees that extend across input sizes, as we verify empirically.
Provably Efficient Third-Person Imitation from Offline Observation
Feb 27, 2020

Abstract:Domain adaptation in imitation learning represents an essential step towards improving generalizability. However, even in the restricted setting of third-person imitation where transfer is between isomorphic Markov Decision Processes, there are no strong guarantees on the performance of transferred policies. We present problem-dependent, statistical learning guarantees for third-person imitation from observation in an offline setting, and a lower bound on performance in the online setting.
Stochastic Optimization of Sorting Networks via Continuous Relaxations
Mar 21, 2019



Abstract:Sorting input objects is an important step in many machine learning pipelines. However, the sorting operator is non-differentiable with respect to its inputs, which prohibits end-to-end gradient-based optimization. In this work, we propose NeuralSort, a general-purpose continuous relaxation of the output of the sorting operator from permutation matrices to the set of unimodal row-stochastic matrices, where every row sums to one and has a distinct arg max. This relaxation permits straight-through optimization of any computational graph involve a sorting operation. Further, we use this relaxation to enable gradient-based stochastic optimization over the combinatorially large space of permutations by deriving a reparameterized gradient estimator for the Plackett-Luce family of distributions over permutations. We demonstrate the usefulness of our framework on three tasks that require learning semantic orderings of high-dimensional objects, including a fully differentiable, parameterized extension of the k-nearest neighbors algorithm.
Graphite: Iterative Generative Modeling of Graphs
Jun 19, 2018

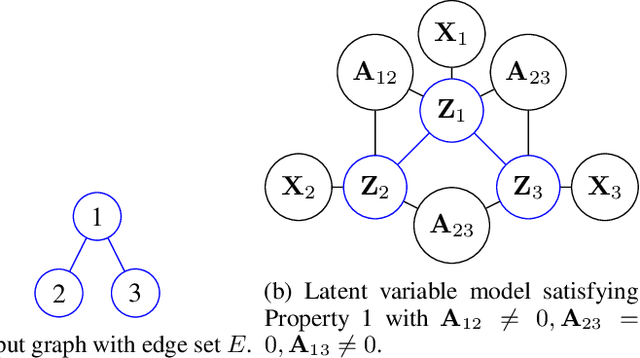
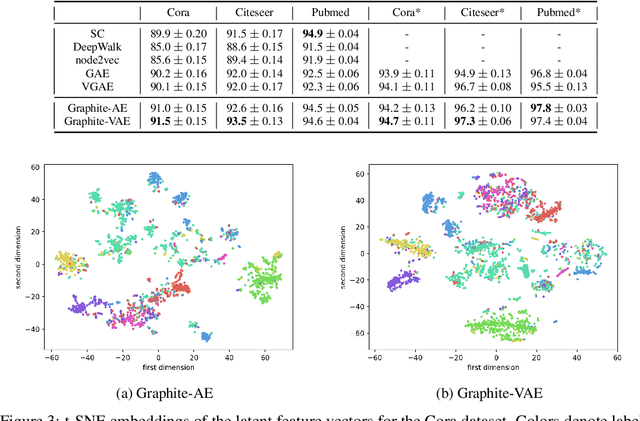
Abstract:Graphs are a fundamental abstraction for modeling relational data. However, graphs are discrete and combinatorial in nature, and learning representations suitable for machine learning tasks poses statistical and computational challenges. In this work, we propose Graphite an algorithmic framework for unsupervised learning of representations over nodes in a graph using deep latent variable generative models. Our model is based on variational autoencoders (VAE), and uses graph neural networks for parameterizing both the generative model (i.e., decoder) and inference model (i.e., encoder). The use of graph neural networks directly incorporates inductive biases due to the spatial, local structure of graphs directly in the generative model. We draw novel connections of our framework with approximate inference via kernel embeddings. Empirically, Graphite outperforms competing approaches for the tasks of density estimation, link prediction, and node classification on synthetic and benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge