Get our free extension to see links to code for papers anywhere online!

Chrome logo Add to Chrome

Firefox logo Add to Firefox
Picture for Creighton Heaukulani

Creighton Heaukulani

Black-box constructions for exchangeable sequences of random multisets


Aug 17, 2019
Creighton Heaukulani, Daniel M. Roy

* 12 pages 
  Access Paper or Ask Questions

Scalable Bayesian dynamic covariance modeling with variational Wishart and inverse Wishart processes


Jun 22, 2019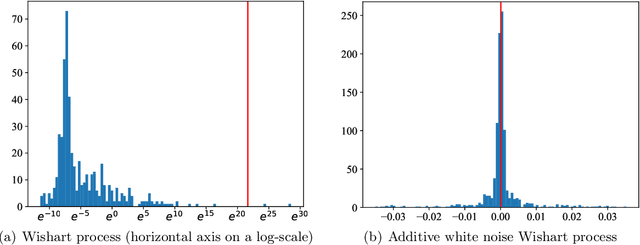
Creighton Heaukulani, Mark van der Wilk

Figure 1 for Scalable Bayesian dynamic covariance modeling with variational Wishart and inverse Wishart processes
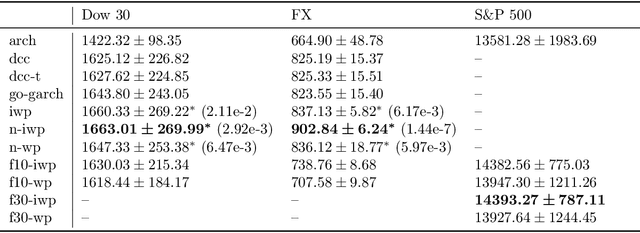
Figure 2 for Scalable Bayesian dynamic covariance modeling with variational Wishart and inverse Wishart processes
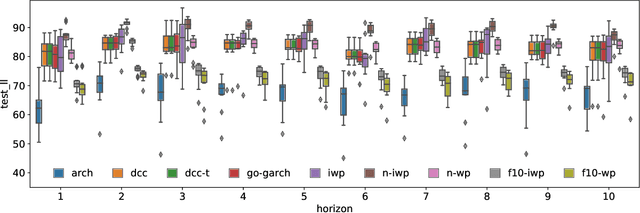
Figure 3 for Scalable Bayesian dynamic covariance modeling with variational Wishart and inverse Wishart processes
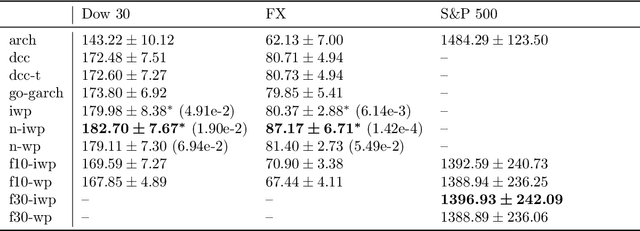
Figure 4 for Scalable Bayesian dynamic covariance modeling with variational Wishart and inverse Wishart processes

  Access Paper or Ask Questions

Variational inference for neural network matrix factorization and its application to stochastic blockmodeling


May 11, 2019
Onno Kampman, Creighton Heaukulani

Figure 1 for Variational inference for neural network matrix factorization and its application to stochastic blockmodeling
Figure 2 for Variational inference for neural network matrix factorization and its application to stochastic blockmodeling

  Access Paper or Ask Questions

Bayesian inference on random simple graphs with power law degree distributions


Jun 18, 2017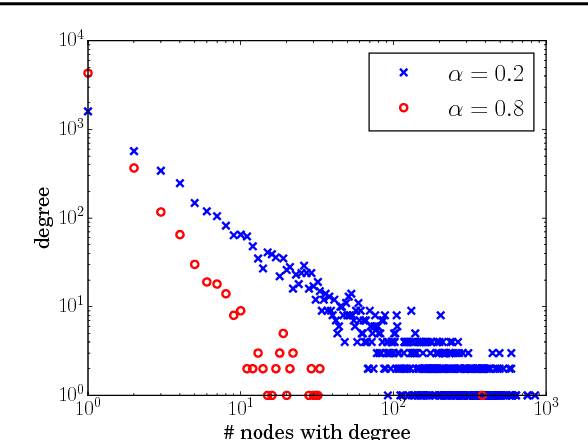
Juho Lee, Creighton Heaukulani, Zoubin Ghahramani, Lancelot F. James, Seungjin Choi

Figure 1 for Bayesian inference on random simple graphs with power law degree distributions
Figure 2 for Bayesian inference on random simple graphs with power law degree distributions
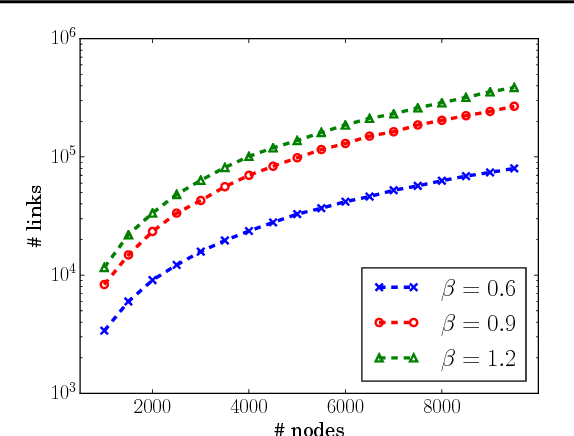
Figure 3 for Bayesian inference on random simple graphs with power law degree distributions
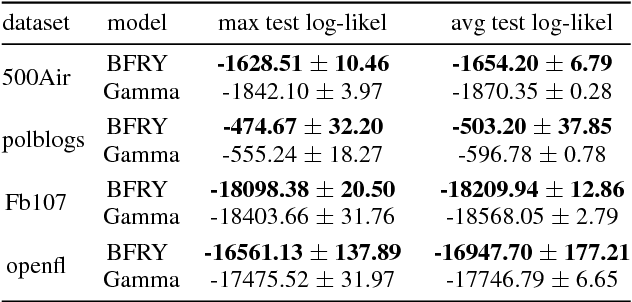
Figure 4 for Bayesian inference on random simple graphs with power law degree distributions

  Access Paper or Ask Questions

The combinatorial structure of beta negative binomial processes


Jun 23, 2016
Creighton Heaukulani, Daniel M. Roy

* Bernoulli 2016, Vol. 22, No. 4, 2301-2324 
 * Published at http://dx.doi.org/10.3150/15-BEJ729 in the Bernoulli (http://isi.cbs.nl/bernoulli/) by the International Statistical Institute/Bernoulli Society (http://isi.cbs.nl/BS/bshome.htm) 
  Access Paper or Ask Questions

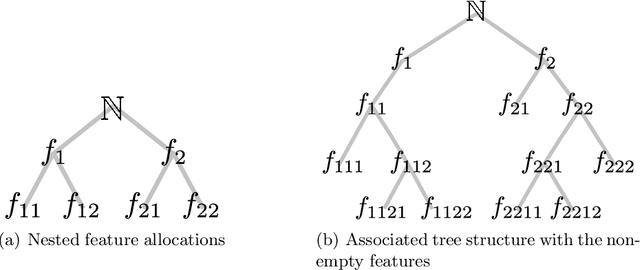
Gibbs-type Indian buffet processes


Dec 08, 2015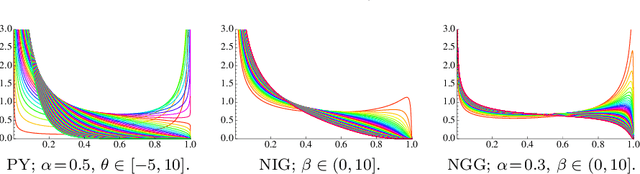
Creighton Heaukulani, Daniel M. Roy

Figure 1 for Gibbs-type Indian buffet processes
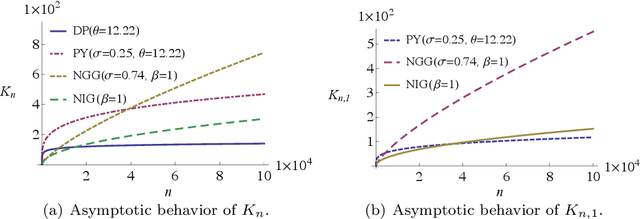
Figure 2 for Gibbs-type Indian buffet processes
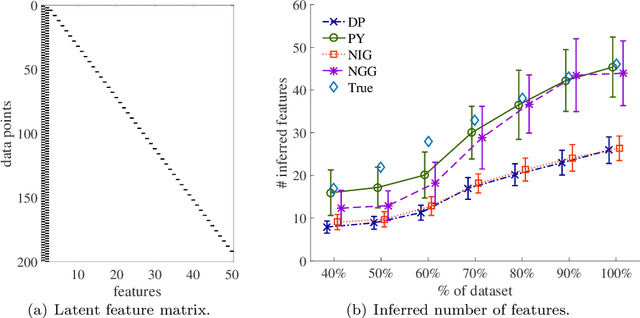
Figure 3 for Gibbs-type Indian buffet processes
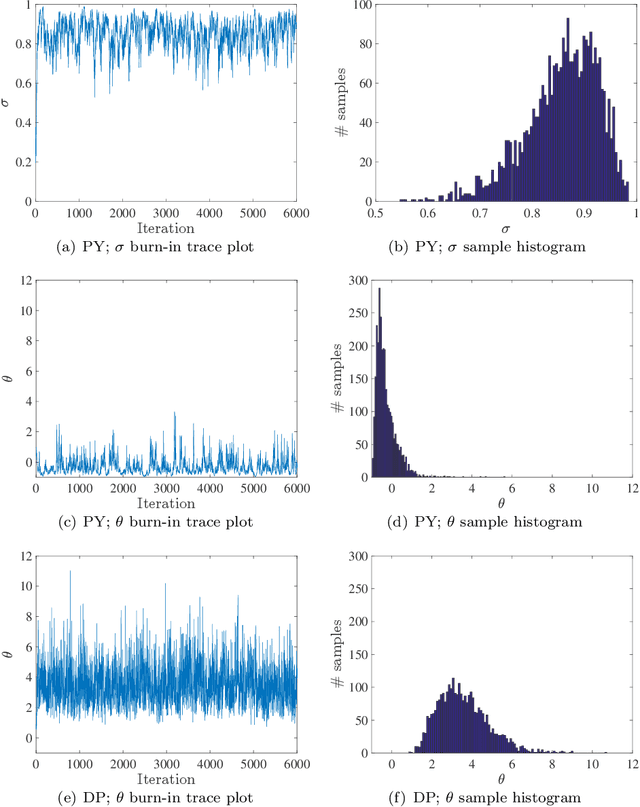
Figure 4 for Gibbs-type Indian buffet processes
* 34 pages, 9 figures 
  Access Paper or Ask Questions

Beta diffusion trees and hierarchical feature allocations


Apr 03, 2015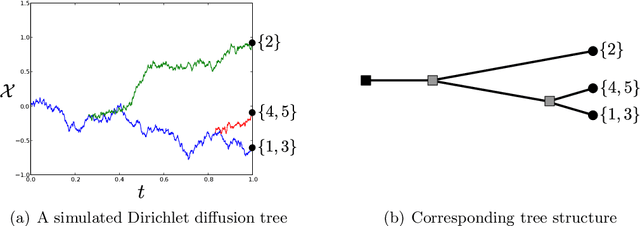
Creighton Heaukulani, David A. Knowles, Zoubin Ghahramani

Figure 1 for Beta diffusion trees and hierarchical feature allocations
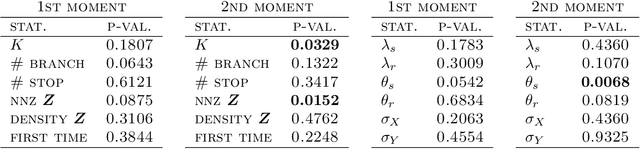
Figure 2 for Beta diffusion trees and hierarchical feature allocations
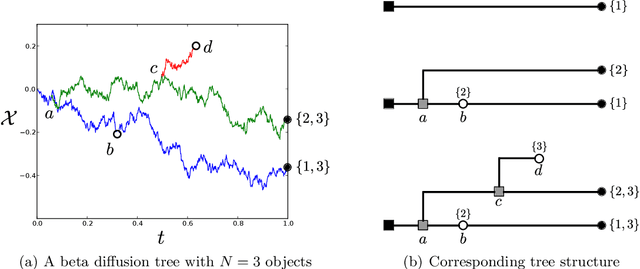
Figure 3 for Beta diffusion trees and hierarchical feature allocations
Figure 4 for Beta diffusion trees and hierarchical feature allocations
* 43 pages, 13 figures. Major revision to the proof of Thm. 2. Large portions of Chs. 2 & 4 moved into the appendix. Added Fig. 4. Revisions throughout 
  Access Paper or Ask Questions