Scalable Bayesian dynamic covariance modeling with variational Wishart and inverse Wishart processes

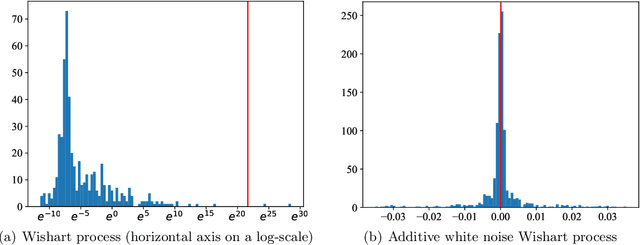
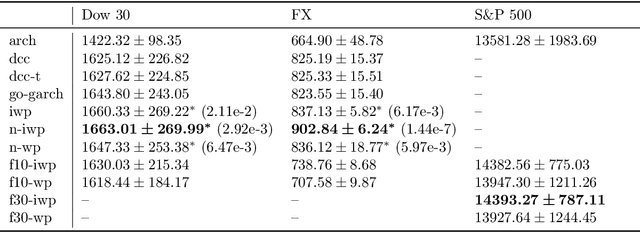
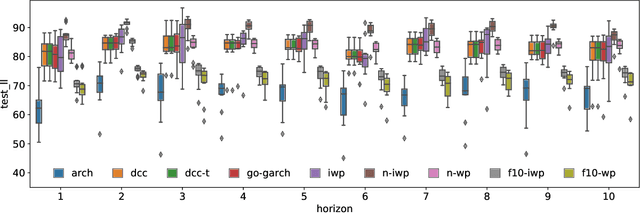
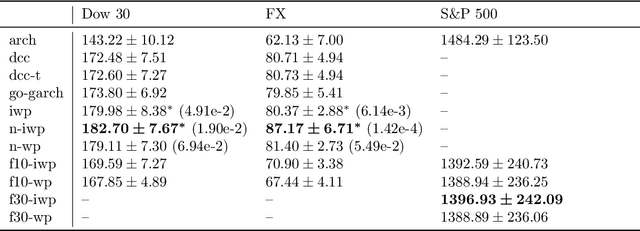
We implement gradient-based variational inference routines for Wishart and inverse Wishart processes, which we apply as Bayesian models for the dynamic, heteroskedastic covariance matrix of a multivariate time series. The Wishart and inverse Wishart processes are constructed from i.i.d. Gaussian processes, for which we apply existing black-box variational inference algorithms for approximate Gaussian process inference. These methods scale well with the length of the time series, however, they fail in the case of the Wishart process, an issue we resolve with a simple modification into an additive white noise parameterization of the model. This modification is also key to implementing a factored variant of the construction, allowing inference to additionally scale to high-dimensional covariance matrices. As with existing MCMC-based inference routines for the Wishart and inverse Wishart processes, we show that these variational alternatives significantly outperform multivariate GARCH baselines when forecasting the covariances of returns on financial instruments.