Poisson Hierarchical Indian Buffet Processes for Within and Across Group Sharing of Latent Features-With Indications for Microbiome Species Sampling Models

In this work, we present a comprehensive Bayesian posterior analysis of what we term Poisson Hierarchical Indian Buffet Processes, designed for complex random sparse count species sampling models that allow for the sharing of information across and within groups. This analysis covers a potentially infinite number of species and unknown parameters, which, within a Bayesian machine learning context, we are able to learn from as more information is sampled. To achieve our refined results, we employ a range of methodologies drawn from Bayesian latent feature models, random occupancy models, and excursion theory. Despite this complexity, our goal is to make our findings accessible to practitioners, including those who may not be familiar with these areas. To facilitate understanding, we adopt a pseudo-expository style that emphasizes clarity and practical utility. We aim to express our findings in a language that resonates with experts in microbiome and ecological studies, addressing gaps in modeling capabilities while acknowledging that we are not experts ourselves in these fields. This approach encourages the use of our models as basic components of more sophisticated frameworks employed by domain experts, embodying the spirit of the seminal work on the Dirichlet Process. Ultimately, our refined posterior analysis not only yields tractable computational procedures but also enables practical statistical implementation and provides a clear mapping to relevant quantities in microbiome analysis.

A Bayesian model for sparse graphs with flexible degree distribution and overlapping community structure

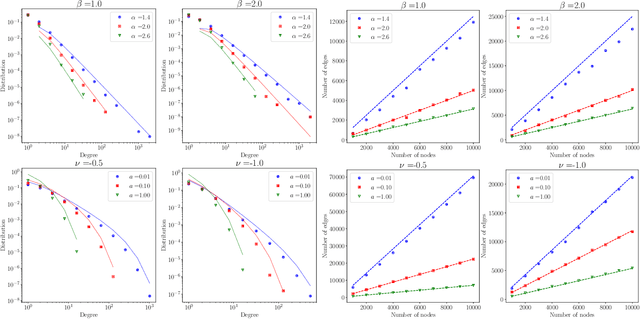
We consider a non-projective class of inhomogeneous random graph models with interpretable parameters and a number of interesting asymptotic properties. Using the results of Bollob\'as et al. [2007], we show that i) the class of models is sparse and ii) depending on the choice of the parameters, the model is either scale-free, with power-law exponent greater than 2, or with an asymptotic degree distribution which is power-law with exponential cut-off. We propose an extension of the model that can accommodate an overlapping community structure. Scalable posterior inference can be performed due to the specific choice of the link probability. We present experiments on five different real-world networks with up to 100,000 nodes and edges, showing that the model can provide a good fit to the degree distribution and recovers well the latent community structure.

Bayesian inference on random simple graphs with power law degree distributions

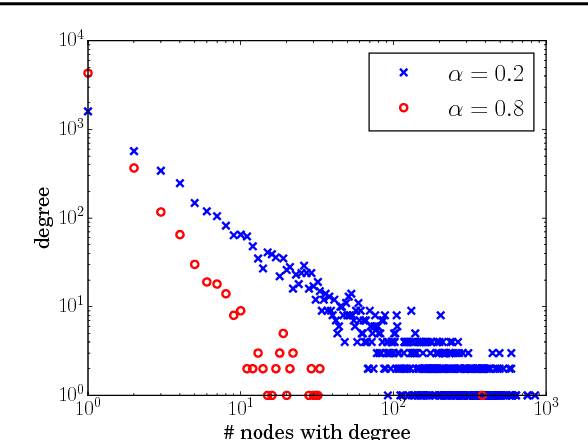
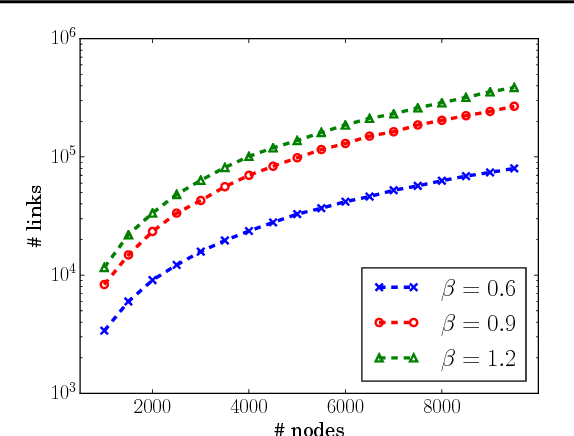
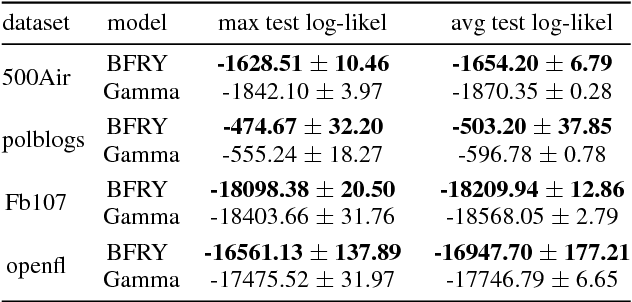
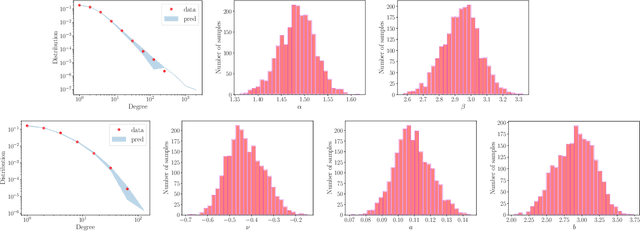
We present a model for random simple graphs with a degree distribution that obeys a power law (i.e., is heavy-tailed). To attain this behavior, the edge probabilities in the graph are constructed from Bertoin-Fujita-Roynette-Yor (BFRY) random variables, which have been recently utilized in Bayesian statistics for the construction of power law models in several applications. Our construction readily extends to capture the structure of latent factors, similarly to stochastic blockmodels, while maintaining its power law degree distribution. The BFRY random variables are well approximated by gamma random variables in a variational Bayesian inference routine, which we apply to several network datasets for which power law degree distributions are a natural assumption. By learning the parameters of the BFRY distribution via probabilistic inference, we are able to automatically select the appropriate power law behavior from the data. In order to further scale our inference procedure, we adopt stochastic gradient ascent routines where the gradients are computed on minibatches (i.e., subsets) of the edges in the graph.