On Uncertainty Estimation by Tree-based Surrogate Models in Sequential Model-based Optimization

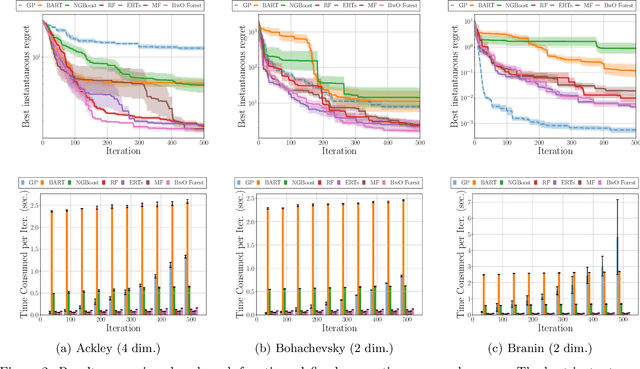
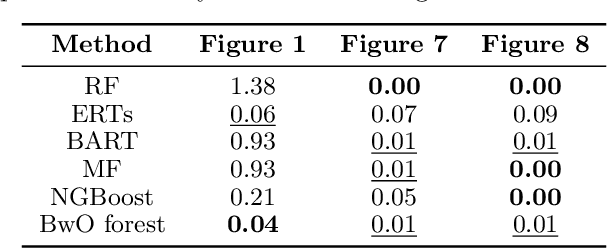
Sequential model-based optimization sequentially selects a candidate point by constructing a surrogate model with the history of evaluations, to solve a black-box optimization problem. Gaussian process (GP) regression is a popular choice as a surrogate model, because of its capability of calculating prediction uncertainty analytically. On the other hand, an ensemble of randomized trees is another option and has practical merits over GPs due to its scalability and easiness of handling continuous/discrete mixed variables. In this paper we revisit various ensembles of randomized trees to investigate their behavior in the perspective of prediction uncertainty estimation. Then, we propose a new way of constructing an ensemble of randomized trees, referred to as BwO forest, where bagging with oversampling is employed to construct bootstrapped samples that are used to build randomized trees with random splitting. Experimental results demonstrate the validity and good performance of BwO forest over existing tree-based models in various circumstances.

Combinatorial Bayesian Optimization with Random Mapping Functions to Convex Polytope

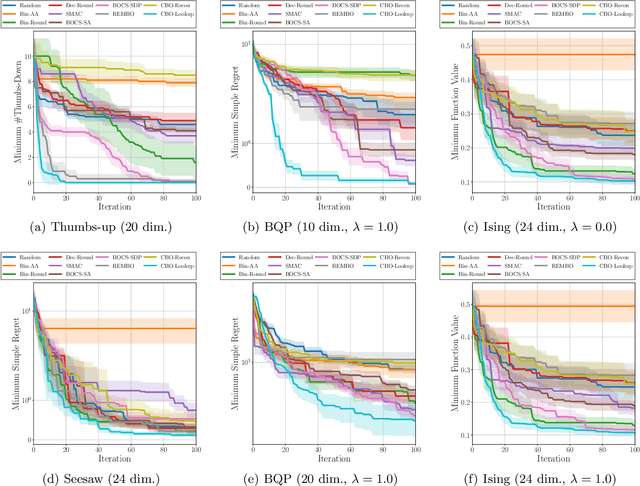
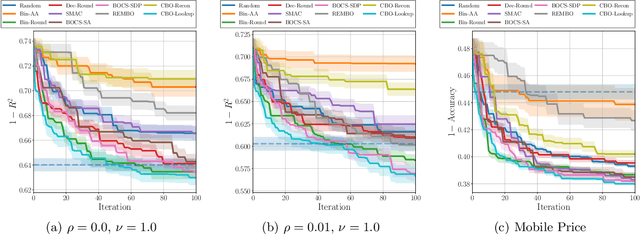
Bayesian optimization is a popular method for solving the problem of global optimization of an expensive-to-evaluate black-box function. It relies on a probabilistic surrogate model of the objective function, upon which an acquisition function is built to determine where next to evaluate the objective function. In general, Bayesian optimization with Gaussian process regression operates on a continuous space. When input variables are categorical or discrete, an extra care is needed. A common approach is to use one-hot encoded or Boolean representation for categorical variables which might yield a {\em combinatorial explosion} problem. In this paper we present a method for Bayesian optimization in a combinatorial space, which can operate well in a large combinatorial space. The main idea is to use a random mapping which embeds the combinatorial space into a convex polytope in a continuous space, on which all essential process is performed to determine a solution to the black-box optimization in the combinatorial space. We describe our {\em combinatorial Bayesian optimization} algorithm and present its regret analysis. Numerical experiments demonstrate that our method outperforms existing methods.

Sparse Network Inversion for Key Instance Detection in Multiple Instance Learning

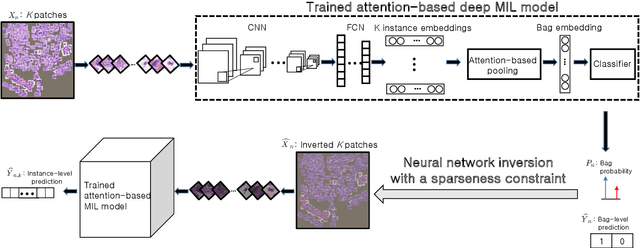
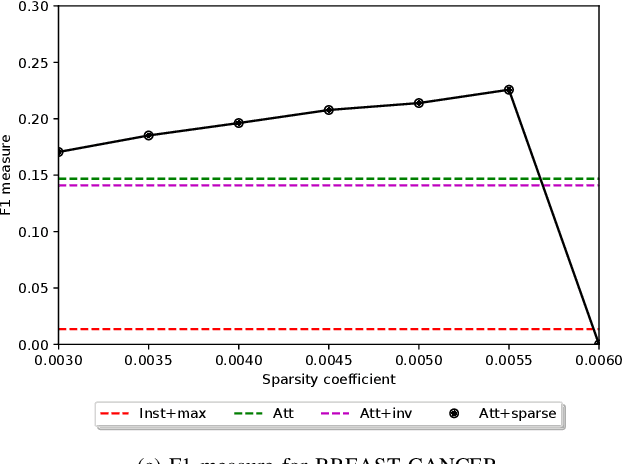
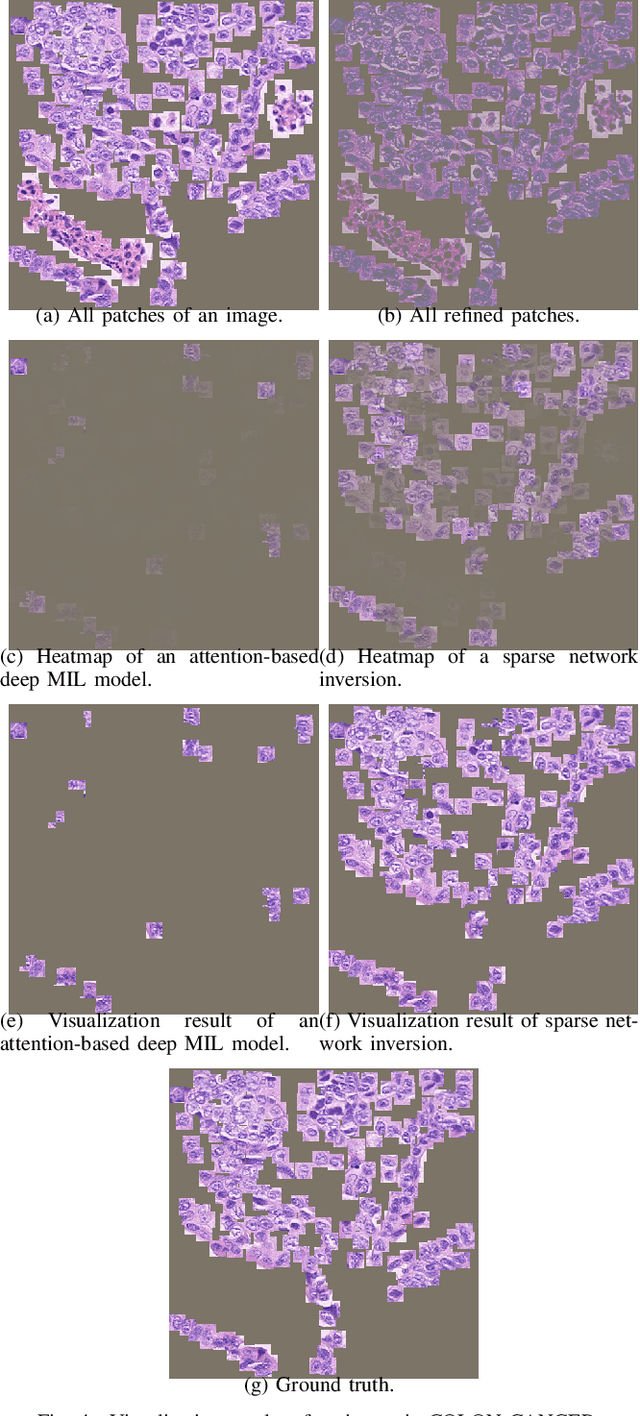
Multiple Instance Learning (MIL) involves predicting a single label for a bag of instances, given positive or negative labels at bag-level, without accessing to label for each instance in the training phase. Since a positive bag contains both positive and negative instances, it is often required to detect positive instances (key instances) when a set of instances is categorized as a positive bag. The attention-based deep MIL model is a recent advance in both bag-level classification and key instance detection (KID). However, if the positive and negative instances in a positive bag are not clearly distinguishable, the attention-based deep MIL model has limited KID performance as the attention scores are skewed to few positive instances. In this paper, we present a method to improve the attention-based deep MIL model in the task of KID. The main idea is to use the neural network inversion to find which instances made contribution to the bag-level prediction produced by the trained MIL model. Moreover, we incorporate a sparseness constraint into the neural network inversion, leading to the sparse network inversion which is solved by the proximal gradient method. Numerical experiments on an MNIST-based image MIL dataset and two real-world histopathology datasets verify the validity of our method, demonstrating the KID performance is significantly improved while the performance of bag-level prediction is maintained.

Neural Complexity Measures

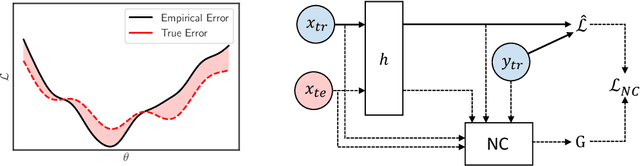
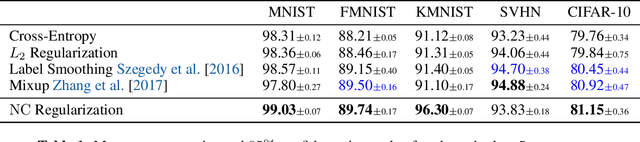
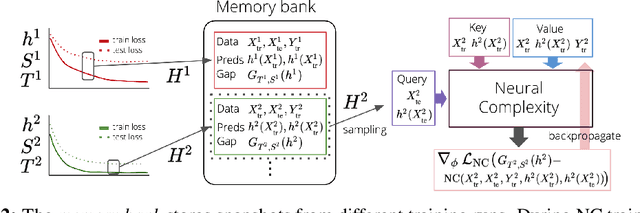
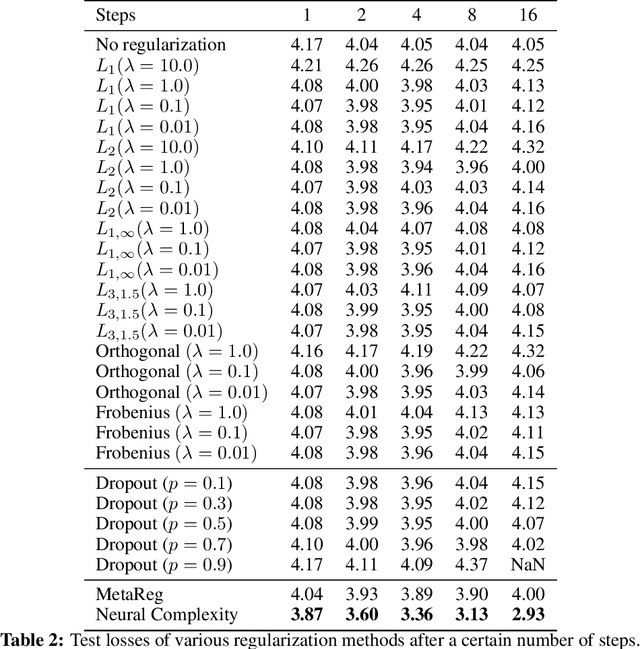
While various complexity measures for diverse model classes have been proposed, specifying an appropriate measure capable of predicting and explaining generalization in deep networks has proven to be challenging. We propose \textit{Neural Complexity} (NC), an alternative data-driven approach that meta-learns a scalar complexity measure through interactions with a large number of heterogeneous tasks. The trained NC model can be added to the standard training loss to regularize any task learner under standard learning frameworks. We contrast NC's approach against existing manually-designed complexity measures and also against other meta-learning models, and validate NC's performance on multiple regression and classification tasks.

Discrete Infomax Codes for Meta-Learning

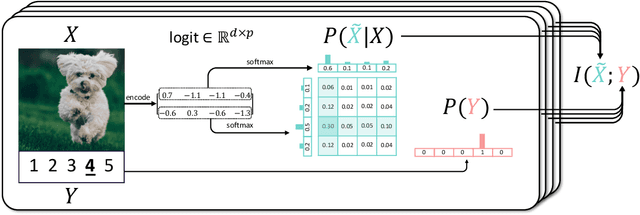
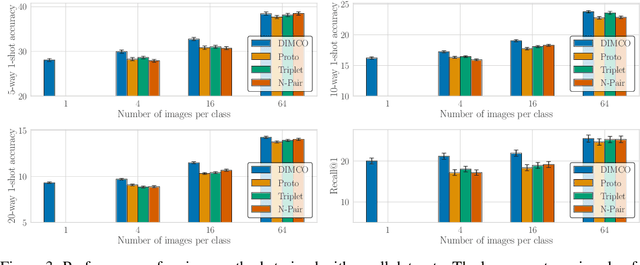
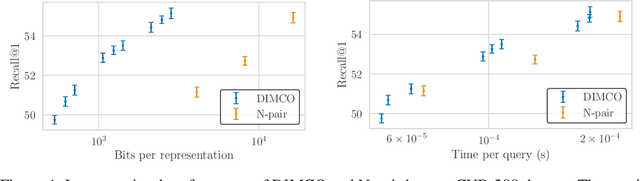
Learning compact discrete representations of data is itself a key task in addition to facilitating subsequent processing. It is also relevant to meta-learning since a latent representation shared across relevant tasks enables a model to adapt to new tasks quickly. In this paper, we present a method for learning a stochastic encoder that yields discrete p-way codes of length d by maximizing the mutual information between representations and labels. We show that previous loss functions for deep metric learning are approximations to this information-theoretic objective function. Our model, Discrete InfoMax Codes (DIMCO), learns to produce a short representation of data that can be used to classify classes with few labeled examples. Our analysis shows that using shorter codes reduces overfitting in the context of few-shot classification. Experiments show that DIMCO requires less memory (i.e., code length) for performance similar to previous methods and that our method is particularly effective when the training dataset is small.

Bayesian Optimization over Sets

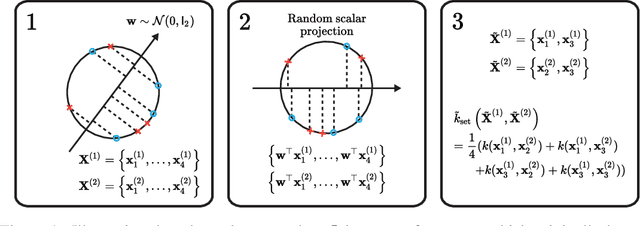
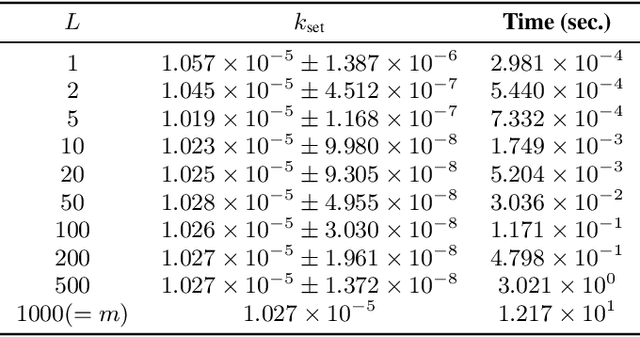
We propose a Bayesian optimization method over sets, to minimize a black-box function that can take a set as single input. Because set inputs are permutation-invariant and variable-length, traditional Gaussian process-based Bayesian optimization strategies which assume vector inputs can fall short. To address this, we develop a Bayesian optimization method with \emph{set kernel} that is used to build surrogate functions. This kernel accumulates similarity over set elements to enforce permutation-invariance and permit sets of variable size, but this comes at a greater computational cost. To reduce this burden, we propose a more efficient probabilistic approximation which we prove is still positive definite and is an unbiased estimator of the true set kernel. Finally, we present several numerical experiments which demonstrate that our method outperforms other methods in various applications.

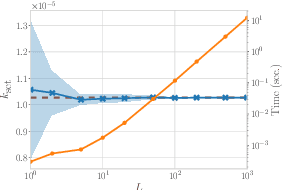
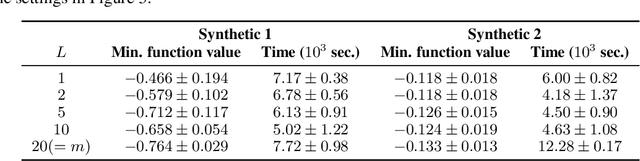
Practical Bayesian Optimization with Threshold-Guided Marginal Likelihood Maximization

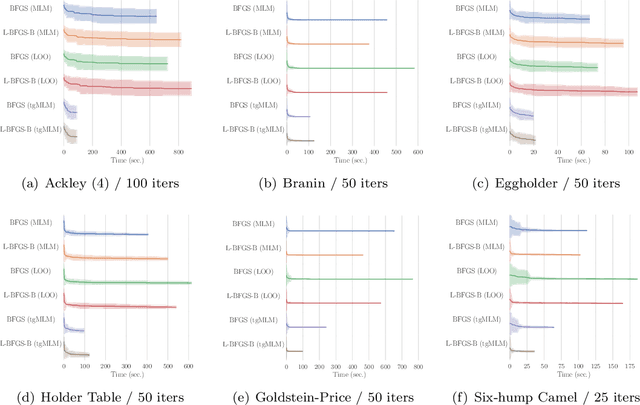
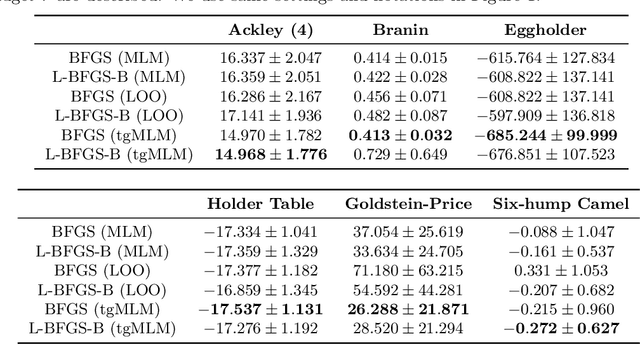
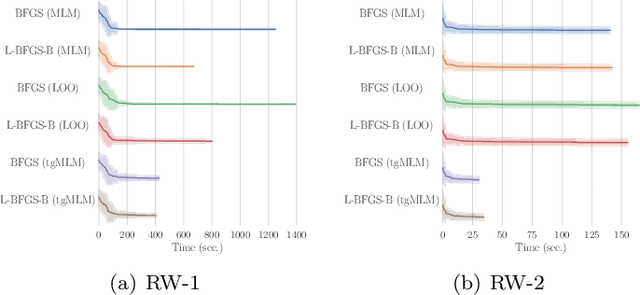
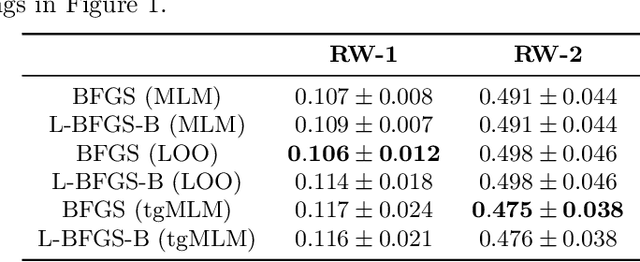
We propose a practical Bayesian optimization method, of which the surrogate function is Gaussian process regression with threshold-guided marginal likelihood maximization. Because Bayesian optimization consumes much time in finding optimal free parameters of Gaussian process regression, mitigating a time complexity of this step is critical to speed up Bayesian optimization. For this reason, we propose a simple, but straightforward Bayesian optimization method, assuming a reasonable condition, which is observed in many practical examples. Our experimental results confirm that our method is effective to reduce the execution time. All implementations are available in our repository.

MxML: Mixture of Meta-Learners for Few-Shot Classification

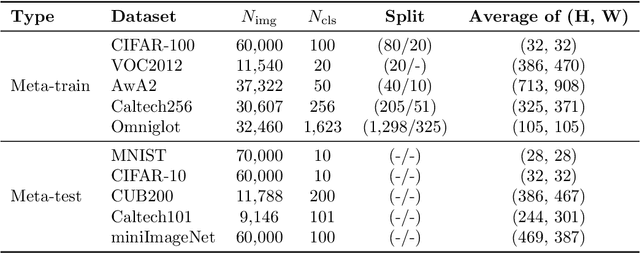
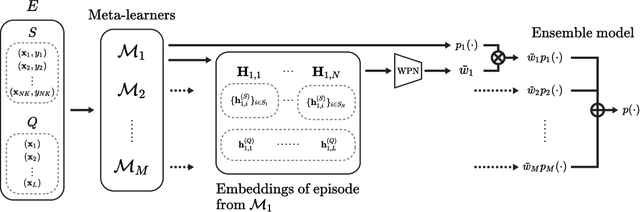
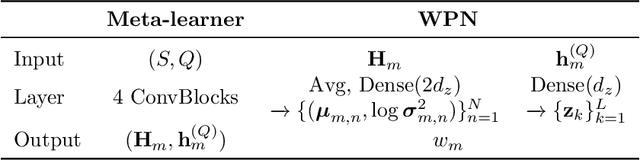
A meta-model is trained on a distribution of similar tasks such that it learns an algorithm that can quickly adapt to a novel task with only a handful of labeled examples. Most of current meta-learning methods assume that the meta-training set consists of relevant tasks sampled from a single distribution. In practice, however, a new task is often out of the task distribution, yielding a performance degradation. One way to tackle this problem is to construct an ensemble of meta-learners such that each meta-learner is trained on different task distribution. In this paper we present a method for constructing a mixture of meta-learners (MxML), where mixing parameters are determined by the weight prediction network (WPN) optimized to improve the few-shot classification performance. Experiments on various datasets demonstrate that MxML significantly outperforms state-of-the-art meta-learners, or their naive ensemble in the case of out-of-distribution as well as in-distribution tasks.

On Local Optimizers of Acquisition Functions in Bayesian Optimization

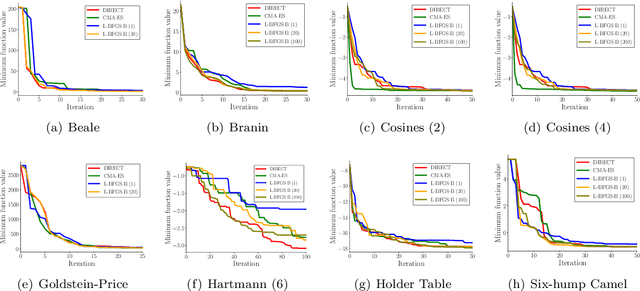
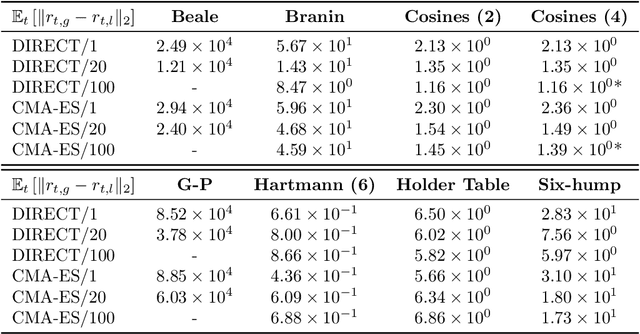
Bayesian optimization is a sample-efficient method for finding a global optimum of an expensive-to-evaluate black-box function. A global solution is found by accumulating a pair of query point and corresponding function value, repeating these two procedures: (i) learning a surrogate model for the objective function using the data observed so far; (ii) the maximization of an acquisition function to determine where next to query the objective function. Convergence guarantees are only valid when the global optimizer of the acquisition function is found and selected as the next query point. In practice, however, local optimizers of acquisition functions are also used, since searching the exact optimizer of the acquisition function is often a non-trivial or time-consuming task. In this paper we present an analysis on the behavior of local optimizers of acquisition functions, in terms of instantaneous regrets over global optimizers. We also present the performance analysis when multi-started local optimizers are used to find the maximum of the acquisition function. Numerical experiments confirm the validity of our theoretical analysis.

Learning to Warm-Start Bayesian Hyperparameter Optimization

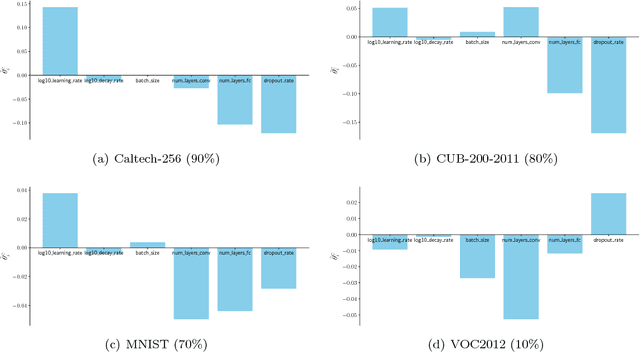
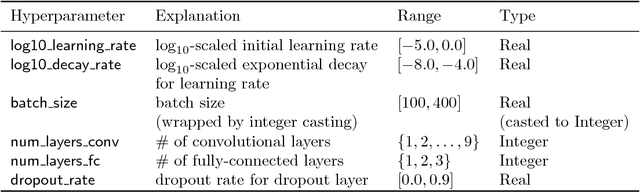
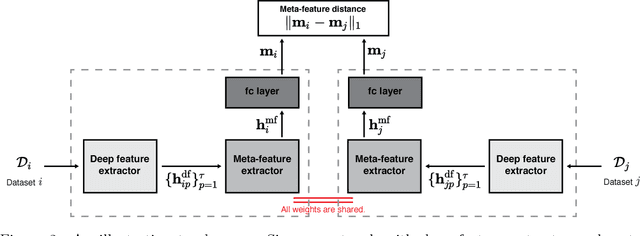
Hyperparameter optimization aims to find the optimal hyperparameter configuration of a machine learning model, which provides the best performance on a validation dataset. Manual search usually leads to get stuck in a local hyperparameter configuration, and heavily depends on human intuition and experience. A simple alternative of manual search is random/grid search on a space of hyperparameters, which still undergoes extensive evaluations of validation errors in order to find its best configuration. Bayesian optimization that is a global optimization method for black-box functions is now popular for hyperparameter optimization, since it greatly reduces the number of validation error evaluations required, compared to random/grid search. Bayesian optimization generally finds the best hyperparameter configuration from random initialization without any prior knowledge. This motivates us to let Bayesian optimization start from the configurations that were successful on similar datasets, which are able to remarkably minimize the number of evaluations. In this paper, we propose deep metric learning to learn meta-features over datasets such that the similarity over them is effectively measured by Euclidean distance between their associated meta-features. To this end, we introduce a Siamese network composed of deep feature and meta-feature extractors, where deep feature extractor provides a semantic representation of each instance in a dataset and meta-feature extractor aggregates a set of deep features to encode a single representation over a dataset. Then, our learned meta-features are used to select a few datasets similar to the new dataset, so that hyperparameters in similar datasets are adopted as initializations to warm-start Bayesian hyperparameter optimization.