Bayesian Optimization over Sets
Paper and Code
May 23, 2019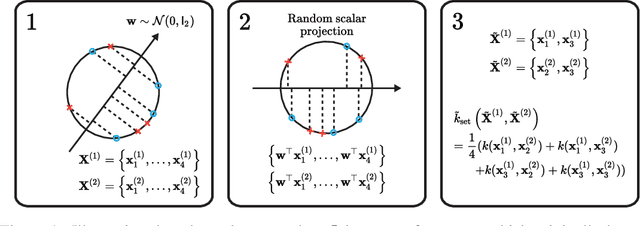
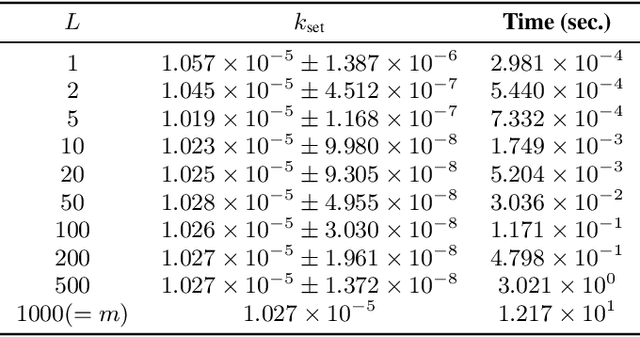
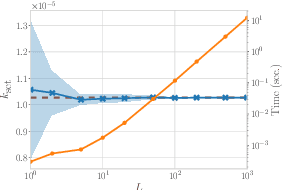
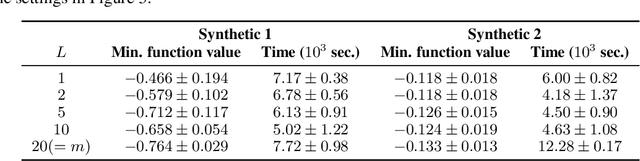
We propose a Bayesian optimization method over sets, to minimize a black-box function that can take a set as single input. Because set inputs are permutation-invariant and variable-length, traditional Gaussian process-based Bayesian optimization strategies which assume vector inputs can fall short. To address this, we develop a Bayesian optimization method with \emph{set kernel} that is used to build surrogate functions. This kernel accumulates similarity over set elements to enforce permutation-invariance and permit sets of variable size, but this comes at a greater computational cost. To reduce this burden, we propose a more efficient probabilistic approximation which we prove is still positive definite and is an unbiased estimator of the true set kernel. Finally, we present several numerical experiments which demonstrate that our method outperforms other methods in various applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge