On Local Optimizers of Acquisition Functions in Bayesian Optimization
Paper and Code
Jan 24, 2019
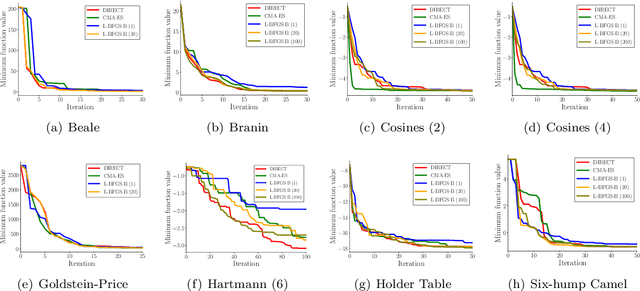
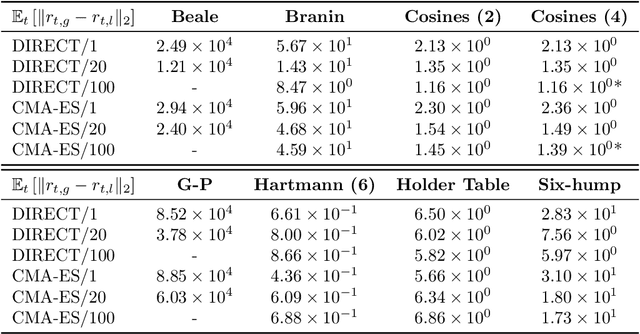
Bayesian optimization is a sample-efficient method for finding a global optimum of an expensive-to-evaluate black-box function. A global solution is found by accumulating a pair of query point and corresponding function value, repeating these two procedures: (i) learning a surrogate model for the objective function using the data observed so far; (ii) the maximization of an acquisition function to determine where next to query the objective function. Convergence guarantees are only valid when the global optimizer of the acquisition function is found and selected as the next query point. In practice, however, local optimizers of acquisition functions are also used, since searching the exact optimizer of the acquisition function is often a non-trivial or time-consuming task. In this paper we present an analysis on the behavior of local optimizers of acquisition functions, in terms of instantaneous regrets over global optimizers. We also present the performance analysis when multi-started local optimizers are used to find the maximum of the acquisition function. Numerical experiments confirm the validity of our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge