Random projections of random manifolds

Interesting data often concentrate on low dimensional smooth manifolds inside a high dimensional ambient space. Random projections are a simple, powerful tool for dimensionality reduction of such data. Previous works have studied bounds on how many projections are needed to accurately preserve the geometry of these manifolds, given their intrinsic dimensionality, volume and curvature. However, such works employ definitions of volume and curvature that are inherently difficult to compute. Therefore such theory cannot be easily tested against numerical simulations to understand the tightness of the proven bounds. We instead study typical distortions arising in random projections of an ensemble of smooth Gaussian random manifolds. We find explicitly computable, approximate theoretical bounds on the number of projections required to accurately preserve the geometry of these manifolds. Our bounds, while approximate, can only be violated with a probability that is exponentially small in the ambient dimension, and therefore they hold with high probability in cases of practical interest. Moreover, unlike previous work, we test our theoretical bounds against numerical experiments on the actual geometric distortions that typically occur for random projections of random smooth manifolds. We find our bounds are tighter than previous results by several orders of magnitude.

Exponential expressivity in deep neural networks through transient chaos

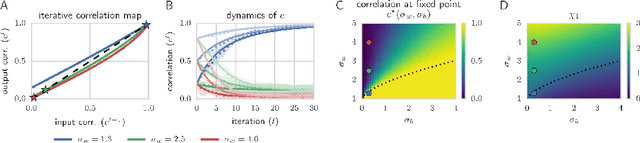
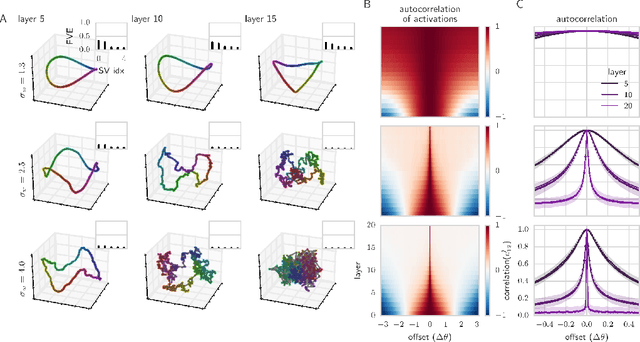
We combine Riemannian geometry with the mean field theory of high dimensional chaos to study the nature of signal propagation in generic, deep neural networks with random weights. Our results reveal an order-to-chaos expressivity phase transition, with networks in the chaotic phase computing nonlinear functions whose global curvature grows exponentially with depth but not width. We prove this generic class of deep random functions cannot be efficiently computed by any shallow network, going beyond prior work restricted to the analysis of single functions. Moreover, we formalize and quantitatively demonstrate the long conjectured idea that deep networks can disentangle highly curved manifolds in input space into flat manifolds in hidden space. Our theoretical analysis of the expressive power of deep networks broadly applies to arbitrary nonlinearities, and provides a quantitative underpinning for previously abstract notions about the geometry of deep functions.

A universal tradeoff between power, precision and speed in physical communication

Maximizing the speed and precision of communication while minimizing power dissipation is a fundamental engineering design goal. Also, biological systems achieve remarkable speed, precision and power efficiency using poorly understood physical design principles. Powerful theories like information theory and thermodynamics do not provide general limits on power, precision and speed. Here we go beyond these classical theories to prove that the product of precision and speed is universally bounded by power dissipation in any physical communication channel whose dynamics is faster than that of the signal. Moreover, our derivation involves a novel connection between friction and information geometry. These results may yield insight into both the engineering design of communication devices and the structure and function of biological signaling systems.

Statistical mechanics of complex neural systems and high dimensional data

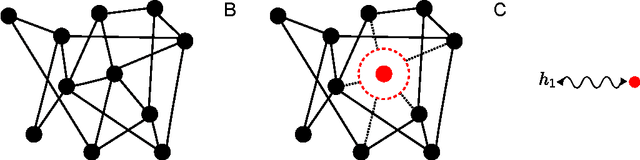
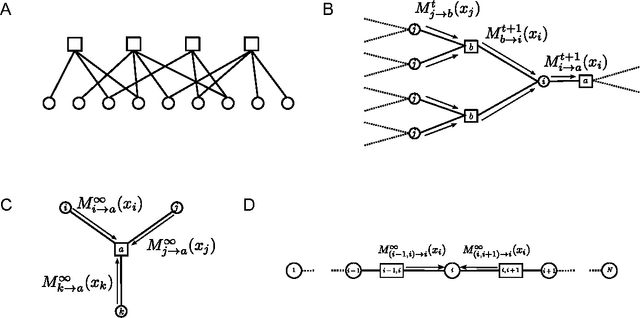
Recent experimental advances in neuroscience have opened new vistas into the immense complexity of neuronal networks. This proliferation of data challenges us on two parallel fronts. First, how can we form adequate theoretical frameworks for understanding how dynamical network processes cooperate across widely disparate spatiotemporal scales to solve important computational problems? And second, how can we extract meaningful models of neuronal systems from high dimensional datasets? To aid in these challenges, we give a pedagogical review of a collection of ideas and theoretical methods arising at the intersection of statistical physics, computer science and neurobiology. We introduce the interrelated replica and cavity methods, which originated in statistical physics as powerful ways to quantitatively analyze large highly heterogeneous systems of many interacting degrees of freedom. We also introduce the closely related notion of message passing in graphical models, which originated in computer science as a distributed algorithm capable of solving large inference and optimization problems involving many coupled variables. We then show how both the statistical physics and computer science perspectives can be applied in a wide diversity of contexts to problems arising in theoretical neuroscience and data analysis. Along the way we discuss spin glasses, learning theory, illusions of structure in noise, random matrices, dimensionality reduction, and compressed sensing, all within the unified formalism of the replica method. Moreover, we review recent conceptual connections between message passing in graphical models, and neural computation and learning. Overall, these ideas illustrate how statistical physics and computer science might provide a lens through which we can uncover emergent computational functions buried deep within the dynamical complexities of neuronal networks.