How JEPA Avoids Noisy Features: The Implicit Bias of Deep Linear Self Distillation Networks

Two competing paradigms exist for self-supervised learning of data representations. Joint Embedding Predictive Architecture (JEPA) is a class of architectures in which semantically similar inputs are encoded into representations that are predictive of each other. A recent successful approach that falls under the JEPA framework is self-distillation, where an online encoder is trained to predict the output of the target encoder, sometimes using a lightweight predictor network. This is contrasted with the Masked AutoEncoder (MAE) paradigm, where an encoder and decoder are trained to reconstruct missing parts of the input in the data space rather, than its latent representation. A common motivation for using the JEPA approach over MAE is that the JEPA objective prioritizes abstract features over fine-grained pixel information (which can be unpredictable and uninformative). In this work, we seek to understand the mechanism behind this empirical observation by analyzing the training dynamics of deep linear models. We uncover a surprising mechanism: in a simplified linear setting where both approaches learn similar representations, JEPAs are biased to learn high-influence features, i.e., features characterized by having high regression coefficients. Our results point to a distinct implicit bias of predicting in latent space that may shed light on its success in practice.

How Far Can Transformers Reason? The Locality Barrier and Inductive Scratchpad

Can Transformers predict new syllogisms by composing established ones? More generally, what type of targets can be learned by such models from scratch? Recent works show that Transformers can be Turing-complete in terms of expressivity, but this does not address the learnability objective. This paper puts forward the notion of 'distribution locality' to capture when weak learning is efficiently achievable by regular Transformers, where the locality measures the least number of tokens required in addition to the tokens histogram to correlate nontrivially with the target. As shown experimentally and theoretically under additional assumptions, distributions with high locality cannot be learned efficiently. In particular, syllogisms cannot be composed on long chains. Furthermore, we show that (i) an agnostic scratchpad cannot help to break the locality barrier, (ii) an educated scratchpad can help if it breaks the locality at each step, (iii) a notion of 'inductive scratchpad' can both break the locality and improve the out-of-distribution generalization, e.g., generalizing to almost double input size for some arithmetic tasks.

LiDAR: Sensing Linear Probing Performance in Joint Embedding SSL Architectures

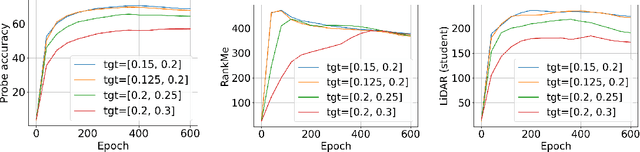
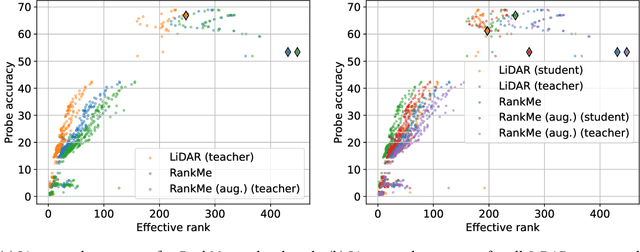
Joint embedding (JE) architectures have emerged as a promising avenue for acquiring transferable data representations. A key obstacle to using JE methods, however, is the inherent challenge of evaluating learned representations without access to a downstream task, and an annotated dataset. Without efficient and reliable evaluation, it is difficult to iterate on architectural and training choices for JE methods. In this paper, we introduce LiDAR (Linear Discriminant Analysis Rank), a metric designed to measure the quality of representations within JE architectures. Our metric addresses several shortcomings of recent approaches based on feature covariance rank by discriminating between informative and uninformative features. In essence, LiDAR quantifies the rank of the Linear Discriminant Analysis (LDA) matrix associated with the surrogate SSL task -- a measure that intuitively captures the information content as it pertains to solving the SSL task. We empirically demonstrate that LiDAR significantly surpasses naive rank based approaches in its predictive power of optimal hyperparameters. Our proposed criterion presents a more robust and intuitive means of assessing the quality of representations within JE architectures, which we hope facilitates broader adoption of these powerful techniques in various domains.

Vanishing Gradients in Reinforcement Finetuning of Language Models

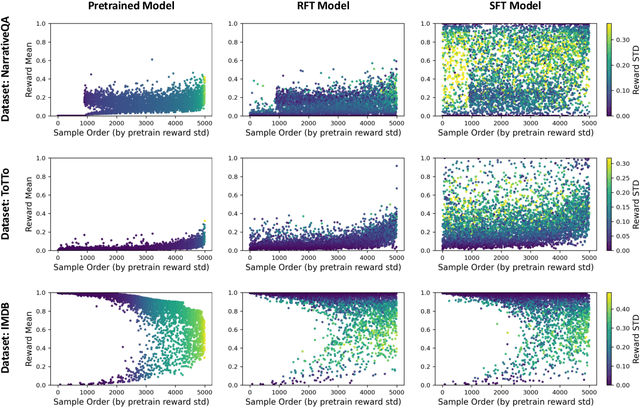
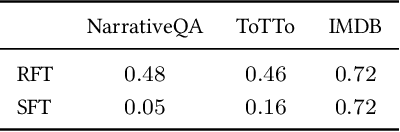
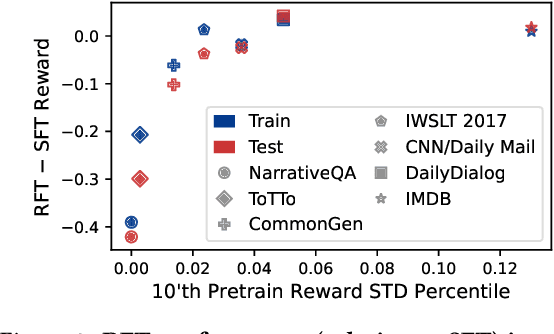
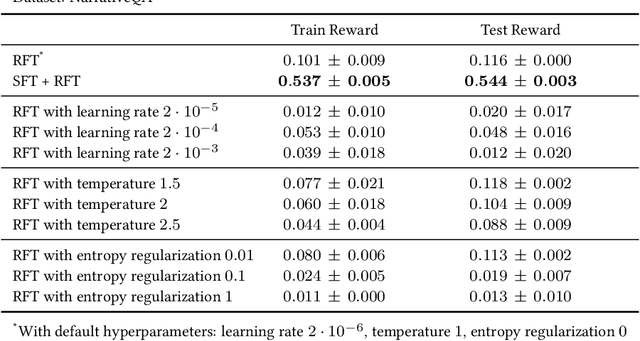
Pretrained language models are commonly aligned with human preferences and downstream tasks via reinforcement finetuning (RFT), which entails maximizing a (possibly learned) reward function using policy gradient algorithms. This work highlights a fundamental optimization obstacle in RFT: we prove that the expected gradient for an input vanishes when its reward standard deviation under the model is small, even if the expected reward is far from optimal. Through experiments on an RFT benchmark and controlled environments, as well as a theoretical analysis, we then demonstrate that vanishing gradients due to small reward standard deviation are prevalent and detrimental, leading to extremely slow reward maximization. Lastly, we explore ways to overcome vanishing gradients in RFT. We find the common practice of an initial supervised finetuning (SFT) phase to be the most promising candidate, which sheds light on its importance in an RFT pipeline. Moreover, we show that a relatively small number of SFT optimization steps on as few as 1% of the input samples can suffice, indicating that the initial SFT phase need not be expensive in terms of compute and data labeling efforts. Overall, our results emphasize that being mindful for inputs whose expected gradient vanishes, as measured by the reward standard deviation, is crucial for successful execution of RFT.

What Algorithms can Transformers Learn? A Study in Length Generalization

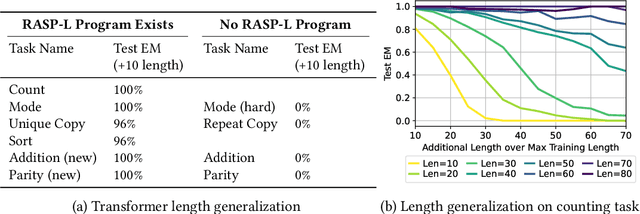
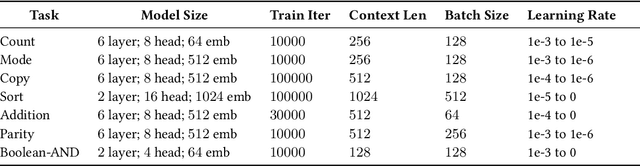
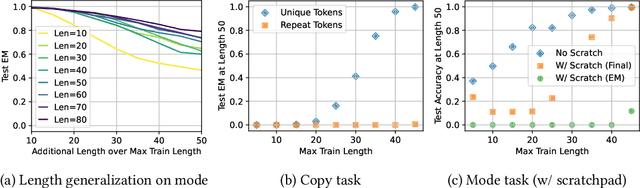
Large language models exhibit surprising emergent generalization properties, yet also struggle on many simple reasoning tasks such as arithmetic and parity. This raises the question of if and when Transformer models can learn the true algorithm for solving a task. We study the scope of Transformers' abilities in the specific setting of length generalization on algorithmic tasks. Here, we propose a unifying framework to understand when and how Transformers can exhibit strong length generalization on a given task. Specifically, we leverage RASP (Weiss et al., 2021) -- a programming language designed for the computational model of a Transformer -- and introduce the RASP-Generalization Conjecture: Transformers tend to length generalize on a task if the task can be solved by a short RASP program which works for all input lengths. This simple conjecture remarkably captures most known instances of length generalization on algorithmic tasks. Moreover, we leverage our insights to drastically improve generalization performance on traditionally hard tasks (such as parity and addition). On the theoretical side, we give a simple example where the "min-degree-interpolator" model of learning from Abbe et al. (2023) does not correctly predict Transformers' out-of-distribution behavior, but our conjecture does. Overall, our work provides a novel perspective on the mechanisms of compositional generalization and the algorithmic capabilities of Transformers.

When can transformers reason with abstract symbols?

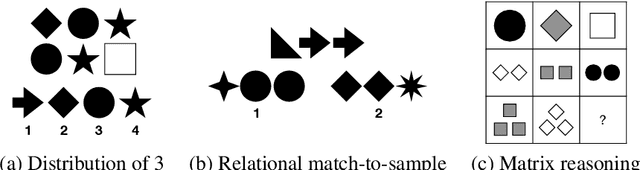
We investigate the capabilities of transformer large language models (LLMs) on relational reasoning tasks involving abstract symbols. Such tasks have long been studied in the neuroscience literature as fundamental building blocks for more complex abilities in programming, mathematics, and verbal reasoning. For (i) regression tasks, we prove that transformers generalize when trained, but require astonishingly large quantities of training data. For (ii) next-token-prediction tasks with symbolic labels, we show an "inverse scaling law": transformers fail to generalize as their embedding dimension increases. For both settings (i) and (ii), we propose subtle transformer modifications which can reduce the amount of data needed by adding two trainable parameters per head.

Adaptivity and Modularity for Efficient Generalization Over Task Complexity

Can transformers generalize efficiently on problems that require dealing with examples with different levels of difficulty? We introduce a new task tailored to assess generalization over different complexities and present results that indicate that standard transformers face challenges in solving these tasks. These tasks are variations of pointer value retrieval previously introduced by Zhang et al. (2021). We investigate how the use of a mechanism for adaptive and modular computation in transformers facilitates the learning of tasks that demand generalization over the number of sequential computation steps (i.e., the depth of the computation graph). Based on our observations, we propose a transformer-based architecture called Hyper-UT, which combines dynamic function generation from hyper networks with adaptive depth from Universal Transformers. This model demonstrates higher accuracy and a fairer allocation of computational resources when generalizing to higher numbers of computation steps. We conclude that mechanisms for adaptive depth and modularity complement each other in improving efficient generalization concerning example complexity. Additionally, to emphasize the broad applicability of our findings, we illustrate that in a standard image recognition task, Hyper- UT's performance matches that of a ViT model but with considerably reduced computational demands (achieving over 70\% average savings by effectively using fewer layers).

The Slingshot Mechanism: An Empirical Study of Adaptive Optimizers and the Grokking Phenomenon

The grokking phenomenon as reported by Power et al. ( arXiv:2201.02177 ) refers to a regime where a long period of overfitting is followed by a seemingly sudden transition to perfect generalization. In this paper, we attempt to reveal the underpinnings of Grokking via a series of empirical studies. Specifically, we uncover an optimization anomaly plaguing adaptive optimizers at extremely late stages of training, referred to as the Slingshot Mechanism. A prominent artifact of the Slingshot Mechanism can be measured by the cyclic phase transitions between stable and unstable training regimes, and can be easily monitored by the cyclic behavior of the norm of the last layers weights. We empirically observe that without explicit regularization, Grokking as reported in ( arXiv:2201.02177 ) almost exclusively happens at the onset of Slingshots, and is absent without it. While common and easily reproduced in more general settings, the Slingshot Mechanism does not follow from any known optimization theories that we are aware of, and can be easily overlooked without an in depth examination. Our work points to a surprising and useful inductive bias of adaptive gradient optimizers at late stages of training, calling for a revised theoretical analysis of their origin.

Implicit Greedy Rank Learning in Autoencoders via Overparameterized Linear Networks

Deep linear networks trained with gradient descent yield low rank solutions, as is typically studied in matrix factorization. In this paper, we take a step further and analyze implicit rank regularization in autoencoders. We show greedy learning of low-rank latent codes induced by a linear sub-network at the autoencoder bottleneck. We further propose orthogonal initialization and principled learning rate adjustment to mitigate sensitivity of training dynamics to spectral prior and linear depth. With linear autoencoders on synthetic data, our method converges stably to ground-truth latent code rank. With nonlinear autoencoders, our method converges to latent ranks optimal for downstream classification and image sampling.

Implicit Acceleration and Feature Learning in Infinitely Wide Neural Networks with Bottlenecks

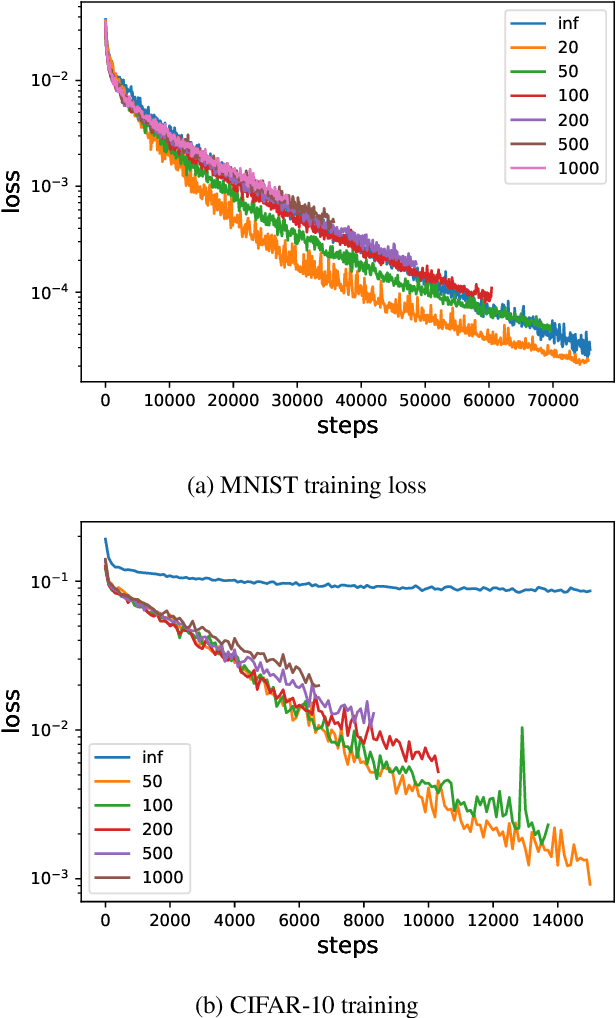
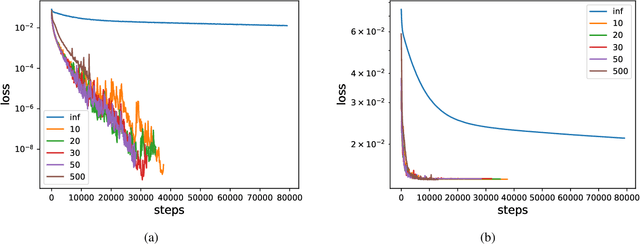
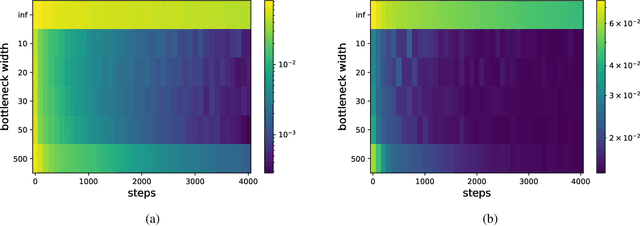
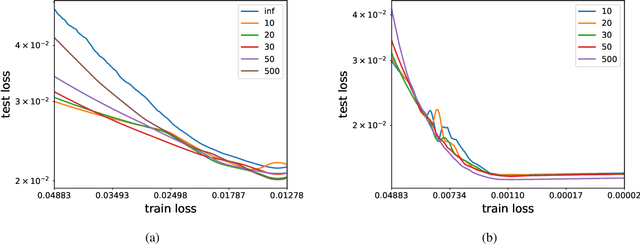
We analyze the learning dynamics of infinitely wide neural networks with a finite sized bottle-neck. Unlike the neural tangent kernel limit, a bottleneck in an otherwise infinite width network al-lows data dependent feature learning in its bottle-neck representation. We empirically show that a single bottleneck in infinite networks dramatically accelerates training when compared to purely in-finite networks, with an improved overall performance. We discuss the acceleration phenomena by drawing similarities to infinitely wide deep linear models, where the acceleration effect of a bottleneck can be understood theoretically.