Shih-Yu Sun
Implicit Greedy Rank Learning in Autoencoders via Overparameterized Linear Networks
Jul 02, 2021



Abstract:Deep linear networks trained with gradient descent yield low rank solutions, as is typically studied in matrix factorization. In this paper, we take a step further and analyze implicit rank regularization in autoencoders. We show greedy learning of low-rank latent codes induced by a linear sub-network at the autoencoder bottleneck. We further propose orthogonal initialization and principled learning rate adjustment to mitigate sensitivity of training dynamics to spectral prior and linear depth. With linear autoencoders on synthetic data, our method converges stably to ground-truth latent code rank. With nonlinear autoencoders, our method converges to latent ranks optimal for downstream classification and image sampling.
Addressing the Loss-Metric Mismatch with Adaptive Loss Alignment
May 15, 2019
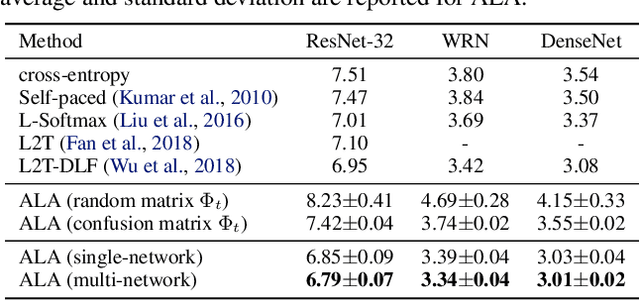
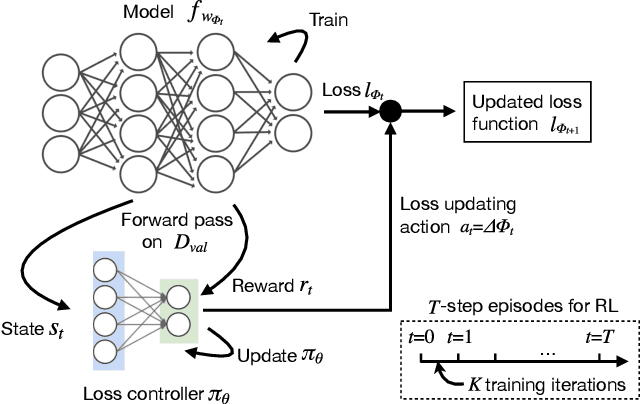

Abstract:In most machine learning training paradigms a fixed, often handcrafted, loss function is assumed to be a good proxy for an underlying evaluation metric. In this work we assess this assumption by meta-learning an adaptive loss function to directly optimize the evaluation metric. We propose a sample efficient reinforcement learning approach for adapting the loss dynamically during training. We empirically show how this formulation improves performance by simultaneously optimizing the evaluation metric and smoothing the loss landscape. We verify our method in metric learning and classification scenarios, showing considerable improvements over the state-of-the-art on a diverse set of tasks. Importantly, our method is applicable to a wide range of loss functions and evaluation metrics. Furthermore, the learned policies are transferable across tasks and data, demonstrating the versatility of the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge