The Implicit Bias of Structured State Space Models Can Be Poisoned With Clean Labels

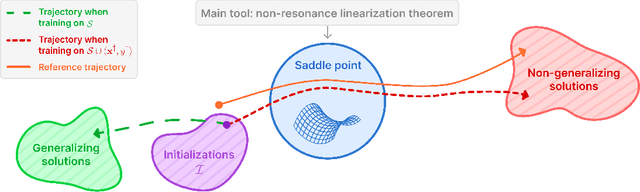
Neural networks are powered by an implicit bias: a tendency of gradient descent to fit training data in a way that generalizes to unseen data. A recent class of neural network models gaining increasing popularity is structured state space models (SSMs), regarded as an efficient alternative to transformers. Prior work argued that the implicit bias of SSMs leads to generalization in a setting where data is generated by a low dimensional teacher. In this paper, we revisit the latter setting, and formally establish a phenomenon entirely undetected by prior work on the implicit bias of SSMs. Namely, we prove that while implicit bias leads to generalization under many choices of training data, there exist special examples whose inclusion in training completely distorts the implicit bias, to a point where generalization fails. This failure occurs despite the special training examples being labeled by the teacher, i.e. having clean labels! We empirically demonstrate the phenomenon, with SSMs trained independently and as part of non-linear neural networks. In the area of adversarial machine learning, disrupting generalization with cleanly labeled training examples is known as clean-label poisoning. Given the proliferation of SSMs, particularly in large language models, we believe significant efforts should be invested in further delineating their susceptibility to clean-label poisoning, and in developing methods for overcoming this susceptibility.

Unintentional Unalignment: Likelihood Displacement in Direct Preference Optimization

Direct Preference Optimization (DPO) and its variants are increasingly used for aligning language models with human preferences. Although these methods are designed to teach a model to generate preferred responses more frequently relative to dispreferred responses, prior work has observed that the likelihood of preferred responses often decreases during training. The current work sheds light on the causes and implications of this counter-intuitive phenomenon, which we term likelihood displacement. We demonstrate that likelihood displacement can be catastrophic, shifting probability mass from preferred responses to responses with an opposite meaning. As a simple example, training a model to prefer $\texttt{No}$ over $\texttt{Never}$ can sharply increase the probability of $\texttt{Yes}$. Moreover, when aligning the model to refuse unsafe prompts, we show that such displacement can unintentionally lead to unalignment, by shifting probability mass from preferred refusal responses to harmful responses (e.g., reducing the refusal rate of Llama-3-8B-Instruct from 74.4% to 33.4%). We theoretically characterize that likelihood displacement is driven by preferences that induce similar embeddings, as measured by a centered hidden embedding similarity (CHES) score. Empirically, the CHES score enables identifying which training samples contribute most to likelihood displacement in a given dataset. Filtering out these samples effectively mitigated unintentional unalignment in our experiments. More broadly, our results highlight the importance of curating data with sufficiently distinct preferences, for which we believe the CHES score may prove valuable.

Lecture Notes on Linear Neural Networks: A Tale of Optimization and Generalization in Deep Learning

These notes are based on a lecture delivered by NC on March 2021, as part of an advanced course in Princeton University on the mathematical understanding of deep learning. They present a theory (developed by NC, NR and collaborators) of linear neural networks -- a fundamental model in the study of optimization and generalization in deep learning. Practical applications born from the presented theory are also discussed. The theory is based on mathematical tools that are dynamical in nature. It showcases the potential of such tools to push the envelope of our understanding of optimization and generalization in deep learning. The text assumes familiarity with the basics of statistical learning theory. Exercises (without solutions) are included.

Understanding Deep Learning via Notions of Rank

Despite the extreme popularity of deep learning in science and industry, its formal understanding is limited. This thesis puts forth notions of rank as key for developing a theory of deep learning, focusing on the fundamental aspects of generalization and expressiveness. In particular, we establish that gradient-based training can induce an implicit regularization towards low rank for several neural network architectures, and demonstrate empirically that this phenomenon may facilitate an explanation of generalization over natural data (e.g., audio, images, and text). Then, we characterize the ability of graph neural networks to model interactions via a notion of rank, which is commonly used for quantifying entanglement in quantum physics. A central tool underlying these results is a connection between neural networks and tensor factorizations. Practical implications of our theory for designing explicit regularization schemes and data preprocessing algorithms are presented.

Implicit Bias of Policy Gradient in Linear Quadratic Control: Extrapolation to Unseen Initial States

In modern machine learning, models can often fit training data in numerous ways, some of which perform well on unseen (test) data, while others do not. Remarkably, in such cases gradient descent frequently exhibits an implicit bias that leads to excellent performance on unseen data. This implicit bias was extensively studied in supervised learning, but is far less understood in optimal control (reinforcement learning). There, learning a controller applied to a system via gradient descent is known as policy gradient, and a question of prime importance is the extent to which a learned controller extrapolates to unseen initial states. This paper theoretically studies the implicit bias of policy gradient in terms of extrapolation to unseen initial states. Focusing on the fundamental Linear Quadratic Regulator (LQR) problem, we establish that the extent of extrapolation depends on the degree of exploration induced by the system when commencing from initial states included in training. Experiments corroborate our theory, and demonstrate its conclusions on problems beyond LQR, where systems are non-linear and controllers are neural networks. We hypothesize that real-world optimal control may be greatly improved by developing methods for informed selection of initial states to train on.

Vanishing Gradients in Reinforcement Finetuning of Language Models

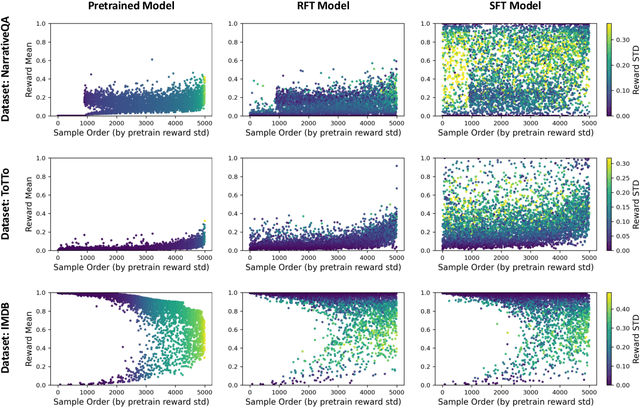
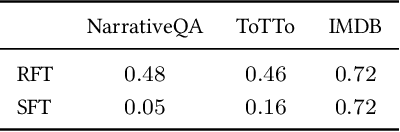
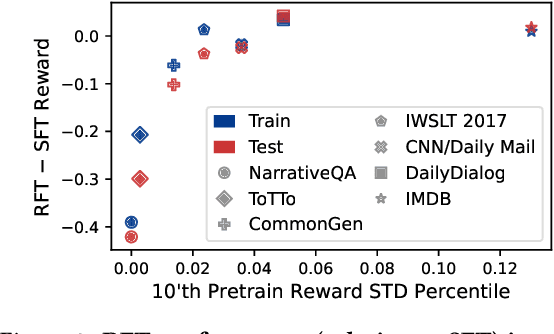
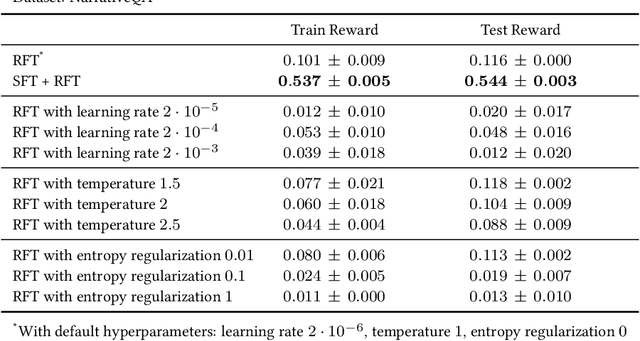
Pretrained language models are commonly aligned with human preferences and downstream tasks via reinforcement finetuning (RFT), which entails maximizing a (possibly learned) reward function using policy gradient algorithms. This work highlights a fundamental optimization obstacle in RFT: we prove that the expected gradient for an input vanishes when its reward standard deviation under the model is small, even if the expected reward is far from optimal. Through experiments on an RFT benchmark and controlled environments, as well as a theoretical analysis, we then demonstrate that vanishing gradients due to small reward standard deviation are prevalent and detrimental, leading to extremely slow reward maximization. Lastly, we explore ways to overcome vanishing gradients in RFT. We find the common practice of an initial supervised finetuning (SFT) phase to be the most promising candidate, which sheds light on its importance in an RFT pipeline. Moreover, we show that a relatively small number of SFT optimization steps on as few as 1% of the input samples can suffice, indicating that the initial SFT phase need not be expensive in terms of compute and data labeling efforts. Overall, our results emphasize that being mindful for inputs whose expected gradient vanishes, as measured by the reward standard deviation, is crucial for successful execution of RFT.

What Algorithms can Transformers Learn? A Study in Length Generalization

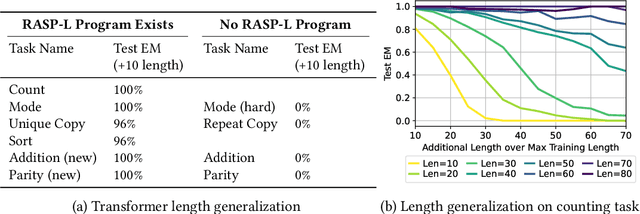
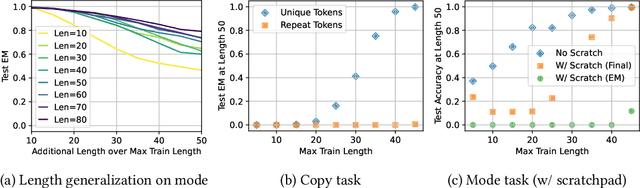
Large language models exhibit surprising emergent generalization properties, yet also struggle on many simple reasoning tasks such as arithmetic and parity. This raises the question of if and when Transformer models can learn the true algorithm for solving a task. We study the scope of Transformers' abilities in the specific setting of length generalization on algorithmic tasks. Here, we propose a unifying framework to understand when and how Transformers can exhibit strong length generalization on a given task. Specifically, we leverage RASP (Weiss et al., 2021) -- a programming language designed for the computational model of a Transformer -- and introduce the RASP-Generalization Conjecture: Transformers tend to length generalize on a task if the task can be solved by a short RASP program which works for all input lengths. This simple conjecture remarkably captures most known instances of length generalization on algorithmic tasks. Moreover, we leverage our insights to drastically improve generalization performance on traditionally hard tasks (such as parity and addition). On the theoretical side, we give a simple example where the "min-degree-interpolator" model of learning from Abbe et al. (2023) does not correctly predict Transformers' out-of-distribution behavior, but our conjecture does. Overall, our work provides a novel perspective on the mechanisms of compositional generalization and the algorithmic capabilities of Transformers.

What Makes Data Suitable for a Locally Connected Neural Network? A Necessary and Sufficient Condition Based on Quantum Entanglement

The question of what makes a data distribution suitable for deep learning is a fundamental open problem. Focusing on locally connected neural networks (a prevalent family of architectures that includes convolutional and recurrent neural networks as well as local self-attention models), we address this problem by adopting theoretical tools from quantum physics. Our main theoretical result states that a certain locally connected neural network is capable of accurate prediction over a data distribution if and only if the data distribution admits low quantum entanglement under certain canonical partitions of features. As a practical application of this result, we derive a preprocessing method for enhancing the suitability of a data distribution to locally connected neural networks. Experiments with widespread models over various datasets demonstrate our findings. We hope that our use of quantum entanglement will encourage further adoption of tools from physics for formally reasoning about the relation between deep learning and real-world data.

On the Ability of Graph Neural Networks to Model Interactions Between Vertices

Graph neural networks (GNNs) are widely used for modeling complex interactions between entities represented as vertices of a graph. Despite recent efforts to theoretically analyze the expressive power of GNNs, a formal characterization of their ability to model interactions is lacking. The current paper aims to address this gap. Formalizing strength of interactions through an established measure known as separation rank, we quantify the ability of certain GNNs to model interaction between a given subset of vertices and its complement, i.e. between sides of a given partition of input vertices. Our results reveal that the ability to model interaction is primarily determined by the partition's walk index -- a graph-theoretical characteristic that we define by the number of walks originating from the boundary of the partition. Experiments with common GNN architectures corroborate this finding. As a practical application of our theory, we design an edge sparsification algorithm named Walk Index Sparsification (WIS), which preserves the ability of a GNN to model interactions when input edges are removed. WIS is simple, computationally efficient, and markedly outperforms alternative methods in terms of induced prediction accuracy. More broadly, it showcases the potential of improving GNNs by theoretically analyzing the interactions they can model.

Implicit Regularization in Hierarchical Tensor Factorization and Deep Convolutional Neural Networks

In the pursuit of explaining implicit regularization in deep learning, prominent focus was given to matrix and tensor factorizations, which correspond to simplified neural networks. It was shown that these models exhibit implicit regularization towards low matrix and tensor ranks, respectively. Drawing closer to practical deep learning, the current paper theoretically analyzes the implicit regularization in hierarchical tensor factorization, a model equivalent to certain deep convolutional neural networks. Through a dynamical systems lens, we overcome challenges associated with hierarchy, and establish implicit regularization towards low hierarchical tensor rank. This translates to an implicit regularization towards locality for the associated convolutional networks. Inspired by our theory, we design explicit regularization discouraging locality, and demonstrate its ability to improve performance of modern convolutional networks on non-local tasks, in defiance of conventional wisdom by which architectural changes are needed. Our work highlights the potential of enhancing neural networks via theoretical analysis of their implicit regularization.