A Formal Framework for Understanding Length Generalization in Transformers

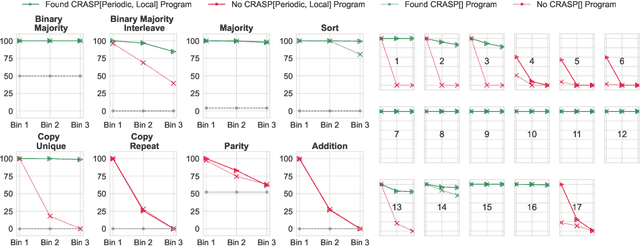
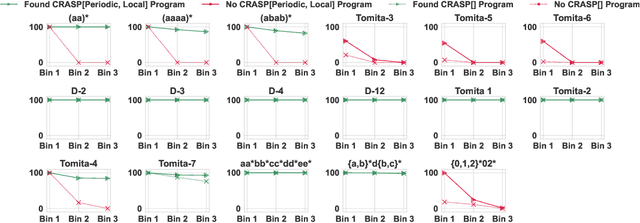
A major challenge for transformers is generalizing to sequences longer than those observed during training. While previous works have empirically shown that transformers can either succeed or fail at length generalization depending on the task, theoretical understanding of this phenomenon remains limited. In this work, we introduce a rigorous theoretical framework to analyze length generalization in causal transformers with learnable absolute positional encodings. In particular, we characterize those functions that are identifiable in the limit from sufficiently long inputs with absolute positional encodings under an idealized inference scheme using a norm-based regularizer. This enables us to prove the possibility of length generalization for a rich family of problems. We experimentally validate the theory as a predictor of success and failure of length generalization across a range of algorithmic and formal language tasks. Our theory not only explains a broad set of empirical observations but also opens the way to provably predicting length generalization capabilities in transformers.

Separations in the Representational Capabilities of Transformers and Recurrent Architectures

Transformer architectures have been widely adopted in foundation models. Due to their high inference costs, there is renewed interest in exploring the potential of efficient recurrent architectures (RNNs). In this paper, we analyze the differences in the representational capabilities of Transformers and RNNs across several tasks of practical relevance, including index lookup, nearest neighbor, recognizing bounded Dyck languages, and string equality. For the tasks considered, our results show separations based on the size of the model required for different architectures. For example, we show that a one-layer Transformer of logarithmic width can perform index lookup, whereas an RNN requires a hidden state of linear size. Conversely, while constant-size RNNs can recognize bounded Dyck languages, we show that one-layer Transformers require a linear size for this task. Furthermore, we show that two-layer Transformers of logarithmic size can perform decision tasks such as string equality or disjointness, whereas both one-layer Transformers and recurrent models require linear size for these tasks. We also show that a log-size two-layer Transformer can implement the nearest neighbor algorithm in its forward pass; on the other hand recurrent models require linear size. Our constructions are based on the existence of $N$ nearly orthogonal vectors in $O(\log N)$ dimensional space and our lower bounds are based on reductions from communication complexity problems. We supplement our theoretical results with experiments that highlight the differences in the performance of these architectures on practical-size sequences.

MAGNIFICo: Evaluating the In-Context Learning Ability of Large Language Models to Generalize to Novel Interpretations

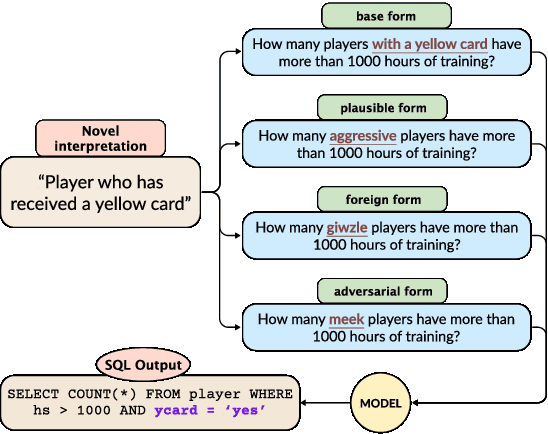
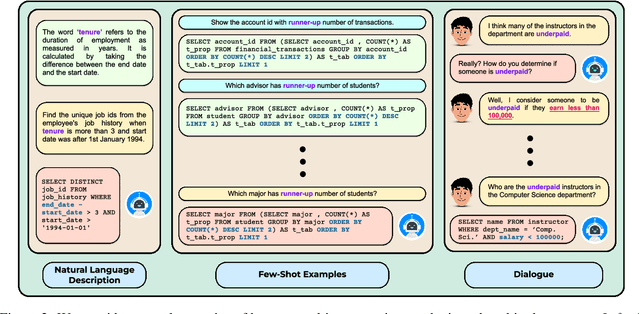
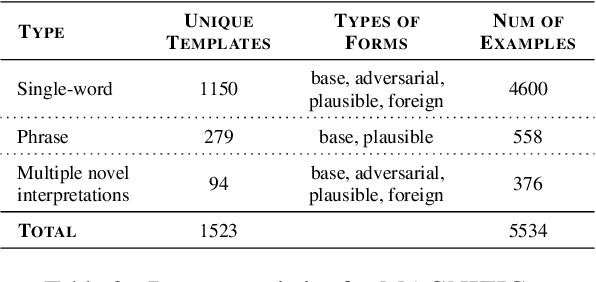
Humans possess a remarkable ability to assign novel interpretations to linguistic expressions, enabling them to learn new words and understand community-specific connotations. However, Large Language Models (LLMs) have a knowledge cutoff and are costly to finetune repeatedly. Therefore, it is crucial for LLMs to learn novel interpretations in-context. In this paper, we systematically analyse the ability of LLMs to acquire novel interpretations using in-context learning. To facilitate our study, we introduce MAGNIFICo, an evaluation suite implemented within a text-to-SQL semantic parsing framework that incorporates diverse tokens and prompt settings to simulate real-world complexity. Experimental results on MAGNIFICo demonstrate that LLMs exhibit a surprisingly robust capacity for comprehending novel interpretations from natural language descriptions as well as from discussions within long conversations. Nevertheless, our findings also highlight the need for further improvements, particularly when interpreting unfamiliar words or when composing multiple novel interpretations simultaneously in the same example. Additionally, our analysis uncovers the semantic predispositions in LLMs and reveals the impact of recency bias for information presented in long contexts.

Understanding In-Context Learning in Transformers and LLMs by Learning to Learn Discrete Functions

In order to understand the in-context learning phenomenon, recent works have adopted a stylized experimental framework and demonstrated that Transformers can learn gradient-based learning algorithms for various classes of real-valued functions. However, the limitations of Transformers in implementing learning algorithms, and their ability to learn other forms of algorithms are not well understood. Additionally, the degree to which these capabilities are confined to attention-based models is unclear. Furthermore, it remains to be seen whether the insights derived from these stylized settings can be extrapolated to pretrained Large Language Models (LLMs). In this work, we take a step towards answering these questions by demonstrating the following: (a) On a test-bed with a variety of Boolean function classes, we find that Transformers can nearly match the optimal learning algorithm for 'simpler' tasks, while their performance deteriorates on more 'complex' tasks. Additionally, we find that certain attention-free models perform (almost) identically to Transformers on a range of tasks. (b) When provided a teaching sequence, i.e. a set of examples that uniquely identifies a function in a class, we show that Transformers learn more sample-efficiently. Interestingly, our results show that Transformers can learn to implement two distinct algorithms to solve a single task, and can adaptively select the more sample-efficient algorithm depending on the sequence of in-context examples. (c) Lastly, we show that extant LLMs, e.g. LLaMA-2, GPT-4, can compete with nearest-neighbor baselines on prediction tasks that are guaranteed to not be in their training set.

Structural Transfer Learning in NL-to-Bash Semantic Parsers

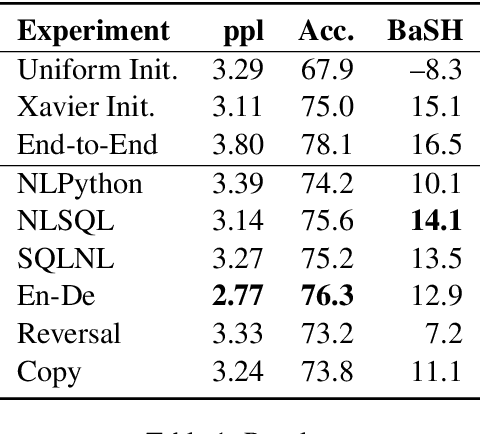
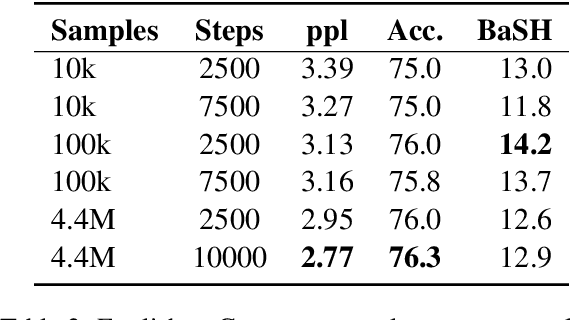
Large-scale pre-training has made progress in many fields of natural language processing, though little is understood about the design of pre-training datasets. We propose a methodology for obtaining a quantitative understanding of structural overlap between machine translation tasks. We apply our methodology to the natural language to Bash semantic parsing task (NLBash) and show that it is largely reducible to lexical alignment. We also find that there is strong structural overlap between NLBash and natural language to SQL. Additionally, we perform a study varying compute expended during pre-training on the English to German machine translation task and find that more compute expended during pre-training does not always correspond semantic representations with stronger transfer to NLBash.

DynaQuant: Compressing Deep Learning Training Checkpoints via Dynamic Quantization

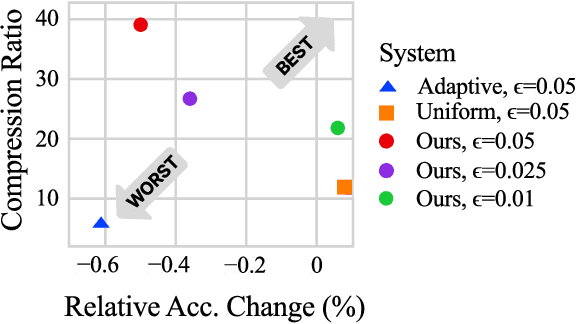
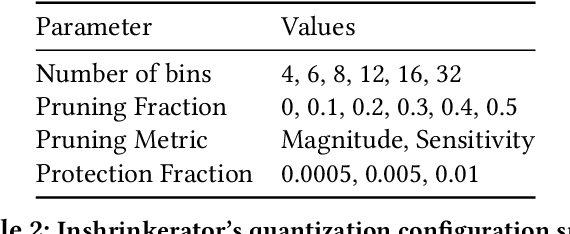
With the increase in the scale of Deep Learning (DL) training workloads in terms of compute resources and time consumption, the likelihood of encountering in-training failures rises substantially, leading to lost work and resource wastage. Such failures are typically offset by a checkpointing mechanism, which comes at the cost of storage and network bandwidth overhead. State-of-the-art approaches involve lossy model compression mechanisms, which induce a tradeoff between the resulting model quality (accuracy) and compression ratio. Delta compression is then also used to further reduce the overhead by only storing the difference between consecutive checkpoints. We make a key enabling observation that the sensitivity of model weights to compression varies during training, and different weights benefit from different quantization levels (ranging from retaining full precision to pruning). We propose (1) a non-uniform quantization scheme that leverages this variation, (2) an efficient search mechanism to dynamically adjust to the best quantization configurations, and (3) a quantization-aware delta compression mechanism that rearranges weights to minimize checkpoint differences, thereby maximizing compression. We instantiate these contributions in DynaQuant - a framework for DL workload checkpoint compression. Our experiments show that DynaQuant consistently achieves better tradeoff between accuracy and compression ratios compared to prior works, enabling a compression ratio up to 39x and withstanding up to 10 restores with negligible accuracy impact for fault-tolerant training. DynaQuant achieves at least an order of magnitude reduction in checkpoint storage overhead for training failure recovery as well as transfer learning use cases without any loss of accuracy

Simplicity Bias in Transformers and their Ability to Learn Sparse Boolean Functions

Despite the widespread success of Transformers on NLP tasks, recent works have found that they struggle to model several formal languages when compared to recurrent models. This raises the question of why Transformers perform well in practice and whether they have any properties that enable them to generalize better than recurrent models. In this work, we conduct an extensive empirical study on Boolean functions to demonstrate the following: (i) Random Transformers are relatively more biased towards functions of low sensitivity. (ii) When trained on Boolean functions, both Transformers and LSTMs prioritize learning functions of low sensitivity, with Transformers ultimately converging to functions of lower sensitivity. (iii) On sparse Boolean functions which have low sensitivity, we find that Transformers generalize near perfectly even in the presence of noisy labels whereas LSTMs overfit and achieve poor generalization accuracy. Overall, our results provide strong quantifiable evidence that suggests differences in the inductive biases of Transformers and recurrent models which may help explain Transformer's effective generalization performance despite relatively limited expressiveness.

Revisiting the Compositional Generalization Abilities of Neural Sequence Models

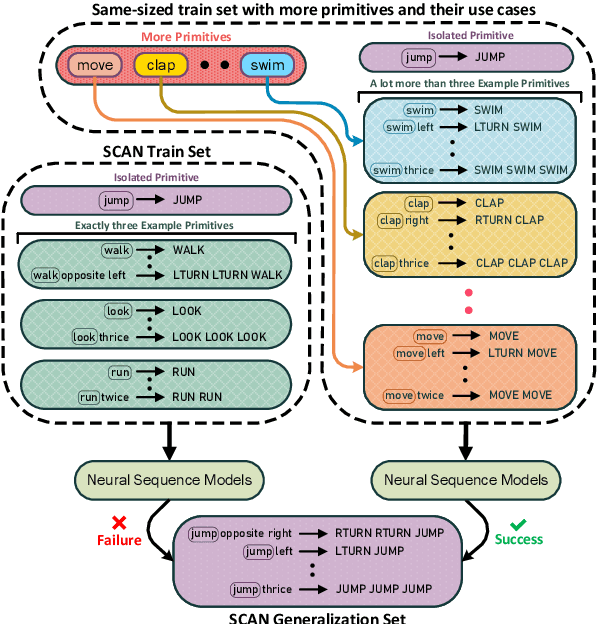
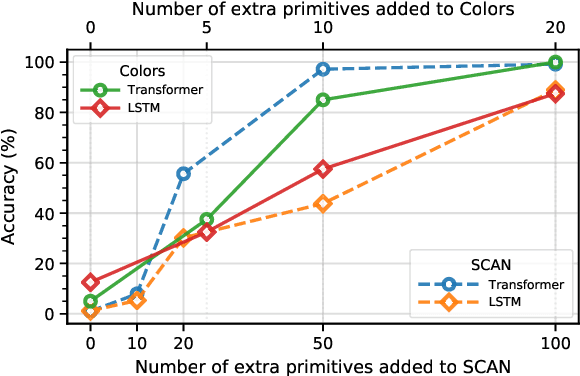
Compositional generalization is a fundamental trait in humans, allowing us to effortlessly combine known phrases to form novel sentences. Recent works have claimed that standard seq-to-seq models severely lack the ability to compositionally generalize. In this paper, we focus on one-shot primitive generalization as introduced by the popular SCAN benchmark. We demonstrate that modifying the training distribution in simple and intuitive ways enables standard seq-to-seq models to achieve near-perfect generalization performance, thereby showing that their compositional generalization abilities were previously underestimated. We perform detailed empirical analysis of this phenomenon. Our results indicate that the generalization performance of models is highly sensitive to the characteristics of the training data which should be carefully considered while designing such benchmarks in future.

Are NLP Models really able to Solve Simple Math Word Problems?

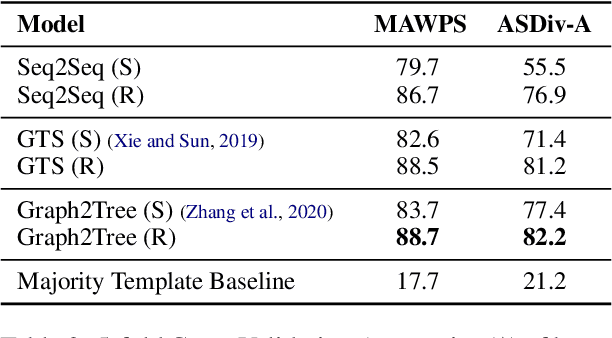
The problem of designing NLP solvers for math word problems (MWP) has seen sustained research activity and steady gains in the test accuracy. Since existing solvers achieve high performance on the benchmark datasets for elementary level MWPs containing one-unknown arithmetic word problems, such problems are often considered "solved" with the bulk of research attention moving to more complex MWPs. In this paper, we restrict our attention to English MWPs taught in grades four and lower. We provide strong evidence that the existing MWP solvers rely on shallow heuristics to achieve high performance on the benchmark datasets. To this end, we show that MWP solvers that do not have access to the question asked in the MWP can still solve a large fraction of MWPs. Similarly, models that treat MWPs as bag-of-words can also achieve surprisingly high accuracy. Further, we introduce a challenge dataset, SVAMP, created by applying carefully chosen variations over examples sampled from existing datasets. The best accuracy achieved by state-of-the-art models is substantially lower on SVAMP, thus showing that much remains to be done even for the simplest of the MWPs.

On the Practical Ability of Recurrent Neural Networks to Recognize Hierarchical Languages

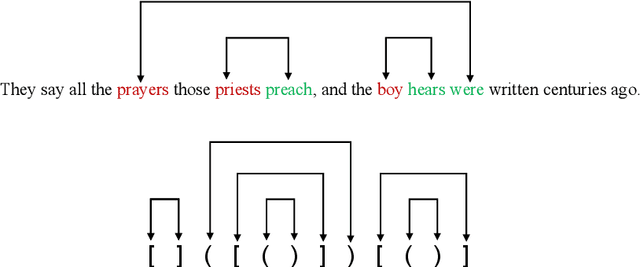
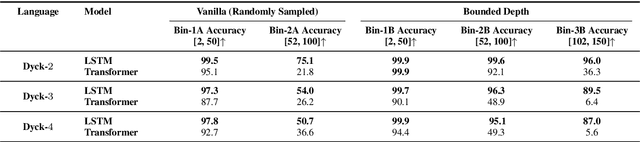
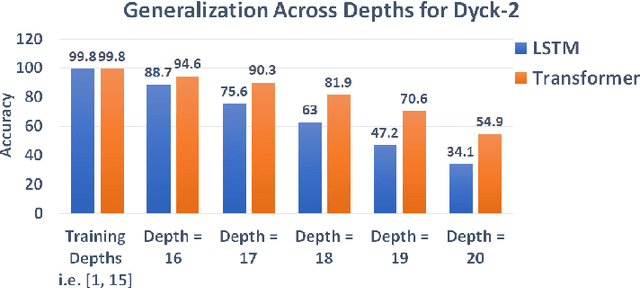
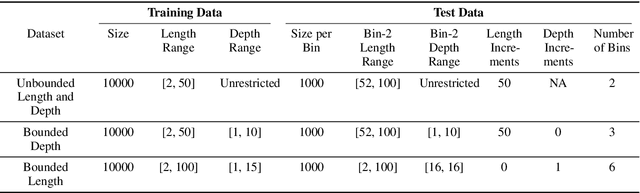
While recurrent models have been effective in NLP tasks, their performance on context-free languages (CFLs) has been found to be quite weak. Given that CFLs are believed to capture important phenomena such as hierarchical structure in natural languages, this discrepancy in performance calls for an explanation. We study the performance of recurrent models on Dyck-n languages, a particularly important and well-studied class of CFLs. We find that while recurrent models generalize nearly perfectly if the lengths of the training and test strings are from the same range, they perform poorly if the test strings are longer. At the same time, we observe that recurrent models are expressive enough to recognize Dyck words of arbitrary lengths in finite precision if their depths are bounded. Hence, we evaluate our models on samples generated from Dyck languages with bounded depth and find that they are indeed able to generalize to much higher lengths. Since natural language datasets have nested dependencies of bounded depth, this may help explain why they perform well in modeling hierarchical dependencies in natural language data despite prior works indicating poor generalization performance on Dyck languages. We perform probing studies to support our results and provide comparisons with Transformers.