Simulating Hard Attention Using Soft Attention

We study conditions under which transformers using soft attention can simulate hard attention, that is, effectively focus all attention on a subset of positions. First, we examine several variants of linear temporal logic, whose formulas have been previously been shown to be computable using hard attention transformers. We demonstrate how soft attention transformers can compute formulas of these logics using unbounded positional embeddings or temperature scaling. Second, we demonstrate how temperature scaling allows softmax transformers to simulate a large subclass of average-hard attention transformers, those that have what we call the uniform-tieless property.

A Formal Framework for Understanding Length Generalization in Transformers

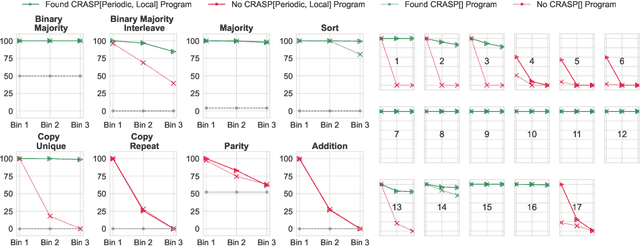
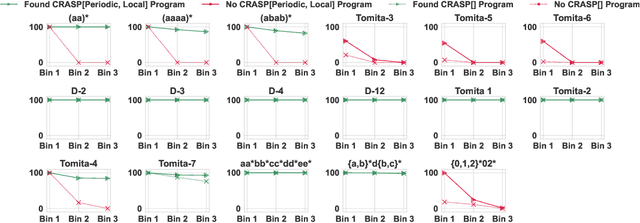
A major challenge for transformers is generalizing to sequences longer than those observed during training. While previous works have empirically shown that transformers can either succeed or fail at length generalization depending on the task, theoretical understanding of this phenomenon remains limited. In this work, we introduce a rigorous theoretical framework to analyze length generalization in causal transformers with learnable absolute positional encodings. In particular, we characterize those functions that are identifiable in the limit from sufficiently long inputs with absolute positional encodings under an idealized inference scheme using a norm-based regularizer. This enables us to prove the possibility of length generalization for a rich family of problems. We experimentally validate the theory as a predictor of success and failure of length generalization across a range of algorithmic and formal language tasks. Our theory not only explains a broad set of empirical observations but also opens the way to provably predicting length generalization capabilities in transformers.

Counting Like Transformers: Compiling Temporal Counting Logic Into Softmax Transformers

Deriving formal bounds on the expressivity of transformers, as well as studying transformers that are constructed to implement known algorithms, are both effective methods for better understanding the computational power of transformers. Towards both ends, we introduce the temporal counting logic $\textbf{K}_\text{t}$[#] alongside the RASP variant $\textbf{C-RASP}$. We show they are equivalent to each other, and that together they are the best-known lower bound on the formal expressivity of future-masked soft attention transformers with unbounded input size. We prove this by showing all $\textbf{K}_\text{t}$[#] formulas can be compiled into these transformers. As a case study, we demonstrate on paper how to use $\textbf{C-RASP}$ to construct simple transformer language models that, using greedy decoding, can only generate sentences that have given properties formally specified in $\textbf{K}_\text{t}$[#].

Masked Hard-Attention Transformers and Boolean RASP Recognize Exactly the Star-Free Languages

We consider transformer encoders with hard attention (in which all attention is focused on exactly one position) and strict future masking (in which each position only attends to positions strictly to its left), and prove that the class of languages recognized by these networks is exactly the star-free languages. Adding position embeddings increases the class of recognized languages to other well-studied classes. A key technique in these proofs is Boolean RASP, a variant of RASP that is restricted to Boolean values. Via the star-free languages, we relate transformers to first-order logic, temporal logic, and algebraic automata theory.