The Bayesian Origin of the Probability Weighting Function in Human Representation of Probabilities

Understanding the representation of probability in the human mind has been of great interest to understanding human decision making. Classical paradoxes in decision making suggest that human perception distorts probability magnitudes. Previous accounts postulate a Probability Weighting Function that transforms perceived probabilities; however, its motivation has been debated. Recent work has sought to motivate this function in terms of noisy representations of probabilities in the human mind. Here, we present an account of the Probability Weighting Function grounded in rational inference over optimal decoding from noisy neural encoding of quantities. We show that our model accurately accounts for behavior in a lottery task and a dot counting task. It further accounts for adaptation to a bimodal short-term prior. Taken together, our results provide a unifying account grounding the human representation of probability in rational inference.

One Size Fits None: Rethinking Fairness in Medical AI

Machine learning (ML) models are increasingly used to support clinical decision-making. However, real-world medical datasets are often noisy, incomplete, and imbalanced, leading to performance disparities across patient subgroups. These differences raise fairness concerns, particularly when they reinforce existing disadvantages for marginalized groups. In this work, we analyze several medical prediction tasks and demonstrate how model performance varies with patient characteristics. While ML models may demonstrate good overall performance, we argue that subgroup-level evaluation is essential before integrating them into clinical workflows. By conducting a performance analysis at the subgroup level, differences can be clearly identified-allowing, on the one hand, for performance disparities to be considered in clinical practice, and on the other hand, for these insights to inform the responsible development of more effective models. Thereby, our work contributes to a practical discussion around the subgroup-sensitive development and deployment of medical ML models and the interconnectedness of fairness and transparency.

Position: Pause Recycling LoRAs and Prioritize Mechanisms to Uncover Limits and Effectiveness

Merging or routing low-rank adapters (LoRAs) has emerged as a popular solution for enhancing large language models, particularly when data access is restricted by regulatory or domain-specific constraints. This position paper argues that the research community should shift its focus from developing new merging or routing algorithms to understanding the conditions under which reusing LoRAs is truly effective. Through theoretical analysis and synthetic two-hop reasoning and math word-problem tasks, we examine whether reusing LoRAs enables genuine compositional generalization or merely reflects shallow pattern matching. Evaluating two data-agnostic methods--parameter averaging and dynamic adapter selection--we found that reusing LoRAs often fails to logically integrate knowledge across disjoint fine-tuning datasets, especially when such knowledge is underrepresented during pretraining. Our empirical results, supported by theoretical insights into LoRA's limited expressiveness, highlight the preconditions and constraints of reusing them for unseen tasks and cast doubt on its feasibility as a truly data-free approach. We advocate for pausing the pursuit of novel methods for recycling LoRAs and emphasize the need for rigorous mechanisms to guide future academic research in adapter-based model merging and practical system designs for practitioners.

Born a Transformer -- Always a Transformer?

Transformers have theoretical limitations in modeling certain sequence-to-sequence tasks, yet it remains largely unclear if these limitations play a role in large-scale pretrained LLMs, or whether LLMs might effectively overcome these constraints in practice due to the scale of both the models themselves and their pretraining data. We explore how these architectural constraints manifest after pretraining, by studying a family of $\textit{retrieval}$ and $\textit{copying}$ tasks inspired by Liu et al. [2024]. We use the recently proposed C-RASP framework for studying length generalization [Huang et al., 2025b] to provide guarantees for each of our settings. Empirically, we observe an $\textit{induction-versus-anti-induction}$ asymmetry, where pretrained models are better at retrieving tokens to the right (induction) rather than the left (anti-induction) of a query token. This asymmetry disappears upon targeted fine-tuning if length-generalization is guaranteed by theory. Mechanistic analysis reveals that this asymmetry is connected to the differences in the strength of induction versus anti-induction circuits within pretrained Transformers. We validate our findings through practical experiments on real-world tasks demonstrating reliability risks. Our results highlight that pretraining selectively enhances certain Transformer capabilities, but does not overcome fundamental length-generalization limits.

Language models can learn implicit multi-hop reasoning, but only if they have lots of training data

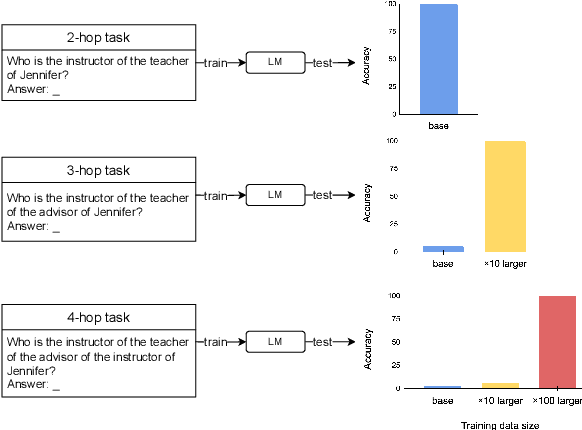
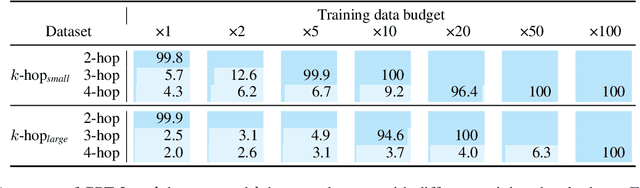
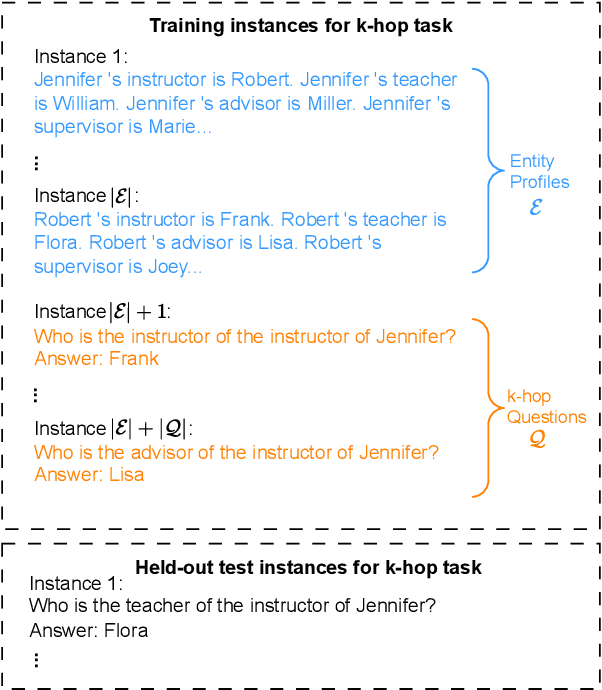
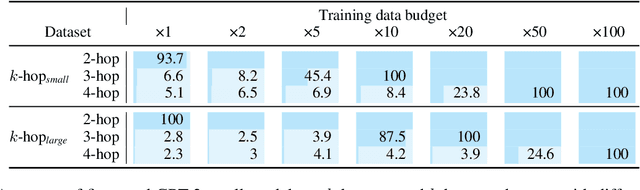
Implicit reasoning is the ability of a language model to solve multi-hop reasoning tasks in a single forward pass, without chain of thought. We investigate this capability using GPT2-style language models trained from scratch on controlled $k$-hop reasoning datasets ($k = 2, 3, 4$). We show that while such models can indeed learn implicit $k$-hop reasoning, the required training data grows exponentially in $k$, and the required number of transformer layers grows linearly in $k$. We offer a theoretical explanation for why this depth growth is necessary. We further find that the data requirement can be mitigated, but not eliminated, through curriculum learning.

Contextualize-then-Aggregate: Circuits for In-Context Learning in Gemma-2 2B

In-Context Learning (ICL) is an intriguing ability of large language models (LLMs). Despite a substantial amount of work on its behavioral aspects and how it emerges in miniature setups, it remains unclear which mechanism assembles task information from the individual examples in a fewshot prompt. We use causal interventions to identify information flow in Gemma-2 2B for five naturalistic ICL tasks. We find that the model infers task information using a two-step strategy we call contextualize-then-aggregate: In the lower layers, the model builds up representations of individual fewshot examples, which are contextualized by preceding examples through connections between fewshot input and output tokens across the sequence. In the higher layers, these representations are aggregated to identify the task and prepare prediction of the next output. The importance of the contextualization step differs between tasks, and it may become more important in the presence of ambiguous examples. Overall, by providing rigorous causal analysis, our results shed light on the mechanisms through which ICL happens in language models.

Lower Bounds for Chain-of-Thought Reasoning in Hard-Attention Transformers

Chain-of-thought reasoning and scratchpads have emerged as critical tools for enhancing the computational capabilities of transformers. While theoretical results show that polynomial-length scratchpads can extend transformers' expressivity from $TC^0$ to $PTIME$, their required length remains poorly understood. Empirical evidence even suggests that transformers need scratchpads even for many problems in $TC^0$, such as Parity or Multiplication, challenging optimistic bounds derived from circuit complexity. In this work, we initiate the study of systematic lower bounds for the number of CoT steps across different algorithmic problems, in the hard-attention regime. We study a variety of algorithmic problems, and provide bounds that are tight up to logarithmic factors. Overall, these results contribute to emerging understanding of the power and limitations of chain-of-thought reasoning.

Emergent Stack Representations in Modeling Counter Languages Using Transformers

Transformer architectures are the backbone of most modern language models, but understanding the inner workings of these models still largely remains an open problem. One way that research in the past has tackled this problem is by isolating the learning capabilities of these architectures by training them over well-understood classes of formal languages. We extend this literature by analyzing models trained over counter languages, which can be modeled using counter variables. We train transformer models on 4 counter languages, and equivalently formulate these languages using stacks, whose depths can be understood as the counter values. We then probe their internal representations for stack depths at each input token to show that these models when trained as next token predictors learn stack-like representations. This brings us closer to understanding the algorithmic details of how transformers learn languages and helps in circuit discovery.

A Formal Framework for Understanding Length Generalization in Transformers

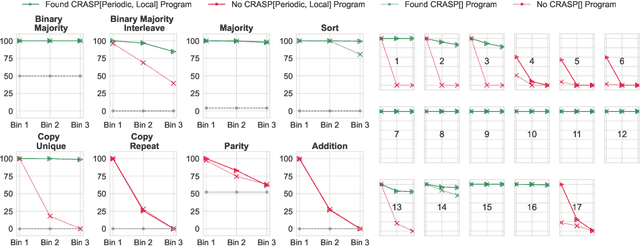
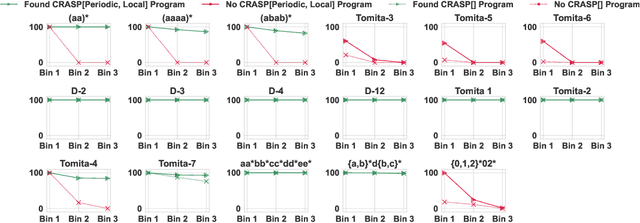
A major challenge for transformers is generalizing to sequences longer than those observed during training. While previous works have empirically shown that transformers can either succeed or fail at length generalization depending on the task, theoretical understanding of this phenomenon remains limited. In this work, we introduce a rigorous theoretical framework to analyze length generalization in causal transformers with learnable absolute positional encodings. In particular, we characterize those functions that are identifiable in the limit from sufficiently long inputs with absolute positional encodings under an idealized inference scheme using a norm-based regularizer. This enables us to prove the possibility of length generalization for a rich family of problems. We experimentally validate the theory as a predictor of success and failure of length generalization across a range of algorithmic and formal language tasks. Our theory not only explains a broad set of empirical observations but also opens the way to provably predicting length generalization capabilities in transformers.

Separations in the Representational Capabilities of Transformers and Recurrent Architectures

Transformer architectures have been widely adopted in foundation models. Due to their high inference costs, there is renewed interest in exploring the potential of efficient recurrent architectures (RNNs). In this paper, we analyze the differences in the representational capabilities of Transformers and RNNs across several tasks of practical relevance, including index lookup, nearest neighbor, recognizing bounded Dyck languages, and string equality. For the tasks considered, our results show separations based on the size of the model required for different architectures. For example, we show that a one-layer Transformer of logarithmic width can perform index lookup, whereas an RNN requires a hidden state of linear size. Conversely, while constant-size RNNs can recognize bounded Dyck languages, we show that one-layer Transformers require a linear size for this task. Furthermore, we show that two-layer Transformers of logarithmic size can perform decision tasks such as string equality or disjointness, whereas both one-layer Transformers and recurrent models require linear size for these tasks. We also show that a log-size two-layer Transformer can implement the nearest neighbor algorithm in its forward pass; on the other hand recurrent models require linear size. Our constructions are based on the existence of $N$ nearly orthogonal vectors in $O(\log N)$ dimensional space and our lower bounds are based on reductions from communication complexity problems. We supplement our theoretical results with experiments that highlight the differences in the performance of these architectures on practical-size sequences.