Maximum Multiscale Entropy and Neural Network Regularization
Paper and Code
Jun 25, 2020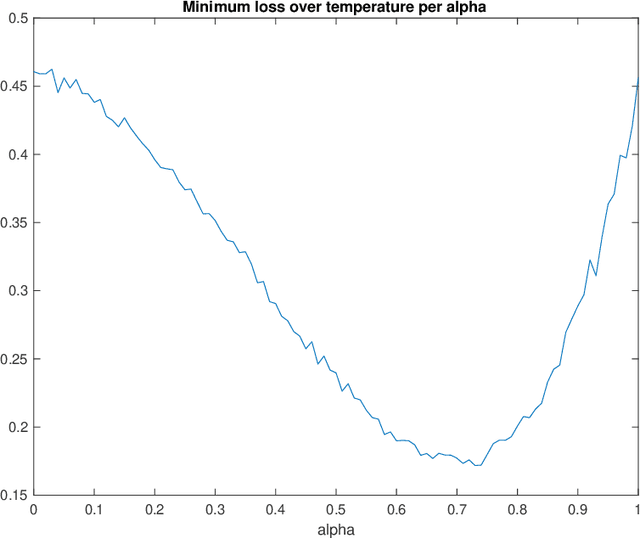
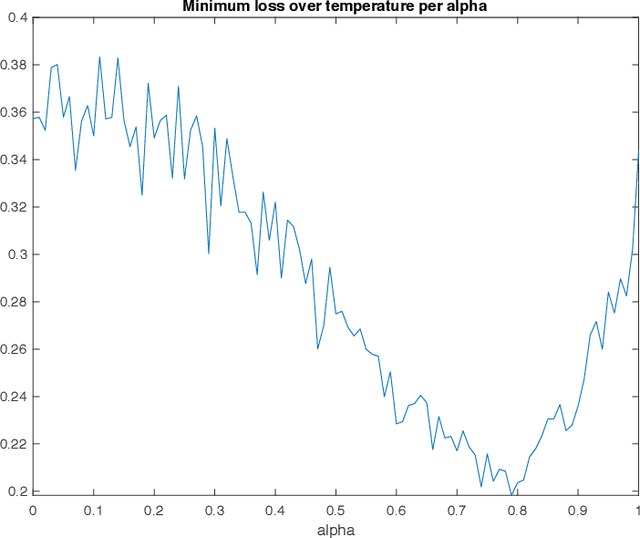
A well-known result across information theory, machine learning, and statistical physics shows that the maximum entropy distribution under a mean constraint has an exponential form called the Gibbs-Boltzmann distribution. This is used for instance in density estimation or to achieve excess risk bounds derived from single-scale entropy regularizers (Xu-Raginsky '17). This paper investigates a generalization of these results to a multiscale setting. We present different ways of generalizing the maximum entropy result by incorporating the notion of scale. For different entropies and arbitrary scale transformations, it is shown that the distribution maximizing a multiscale entropy is characterized by a procedure which has an analogy to the renormalization group procedure in statistical physics. For the case of decimation transformation, it is further shown that this distribution is Gaussian whenever the optimal single-scale distribution is Gaussian. This is then applied to neural networks, and it is shown that in a teacher-student scenario, the multiscale Gibbs posterior can achieve a smaller excess risk than the single-scale Gibbs posterior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge