Chaining Meets Chain Rule: Multilevel Entropic Regularization and Training of Neural Nets
Paper and Code
Jun 26, 2019
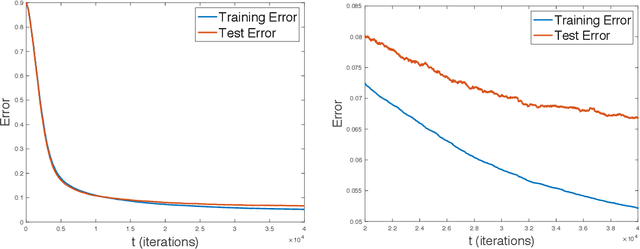
We derive generalization and excess risk bounds for neural nets using a family of complexity measures based on a multilevel relative entropy. The bounds are obtained by introducing the notion of generated hierarchical coverings of neural nets and by using the technique of chaining mutual information introduced in Asadi et al. NeurIPS'18. The resulting bounds are algorithm-dependent and exploit the multilevel structure of neural nets. This, in turn, leads to an empirical risk minimization problem with a multilevel entropic regularization. The minimization problem is resolved by introducing a multi-scale generalization of the celebrated Gibbs posterior distribution, proving that the derived distribution achieves the unique minimum. This leads to a new training procedure for neural nets with performance guarantees, which exploits the chain rule of relative entropy rather than the chain rule of derivatives (as in backpropagation). To obtain an efficient implementation of the latter, we further develop a multilevel Metropolis algorithm simulating the multi-scale Gibbs distribution, with an experiment for a two-layer neural net on the MNIST data set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge