Reverse Lebesgue and Gaussian isoperimetric inequalities for parallel sets with applications
Paper and Code
Jun 16, 2020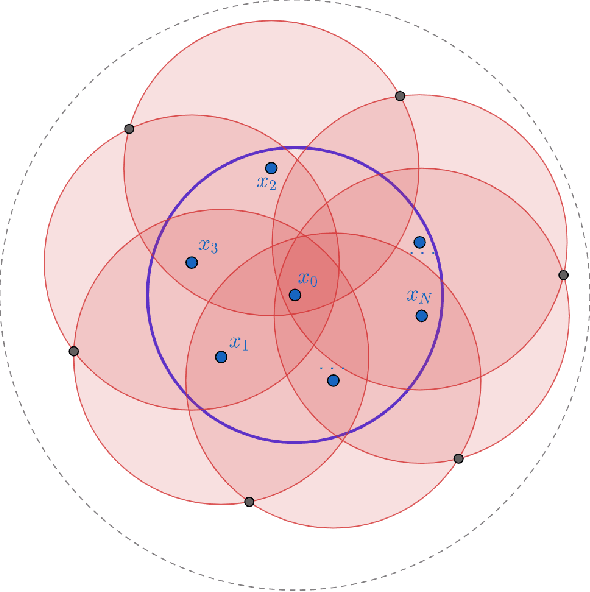
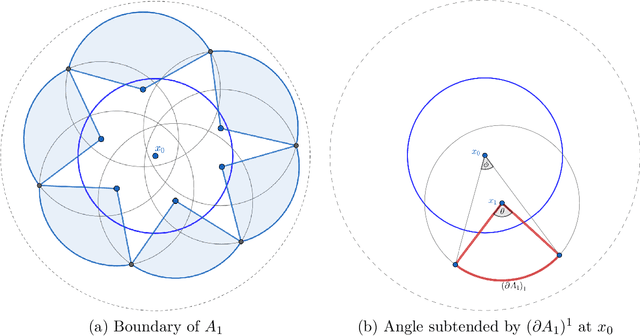
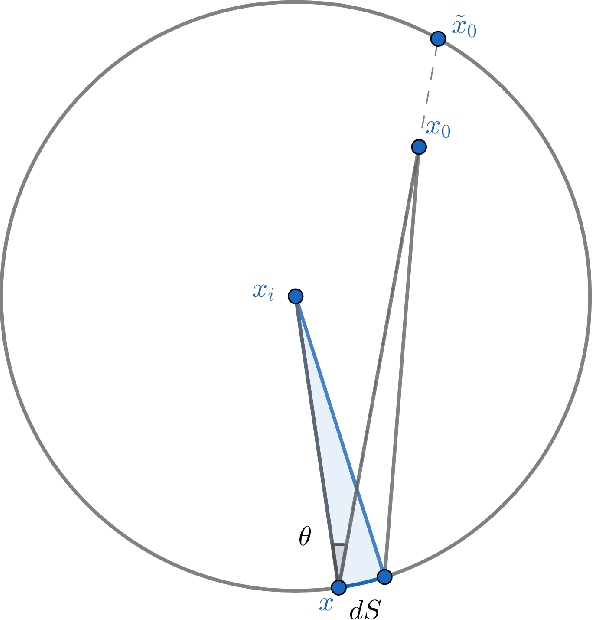
The $r$-parallel set of a measurable set $A \subseteq \mathbb R^d$ is the set of all points whose distance from $A$ is at most $r$. In this paper, we show that the surface area of an $r$-parallel set in $\mathbb R^d$ with volume at most $V$ is upper-bounded by $e^{\Theta(d)}V/r$. We also show that the Gaussian surface area of any $r$-parallel set in $\mathbb R^d$ is upper-bounded by $\max(e^{\Theta(d)}, e^{\Theta(d)}/r)$. We apply our results to two problems in theoretical machine learning: (1) bounding the computational complexity of learning $r$-parallel sets under a Gaussian distribution; and (2) bounding the sample complexity of estimating robust risk, which is a notion of risk in the adversarial machine learning literature that is analogous to the Bayes risk in hypothesis testing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge